毎分 $3\rm cm$ の割合で水面が上がるように $x$ 分間水そうに水を入れる。このときの水面の高さを $y\rm cm$ とするとき、$y$ を $x$ の式で表すと、$\textcolor{blue}{y=3x}$ と表すことができます。
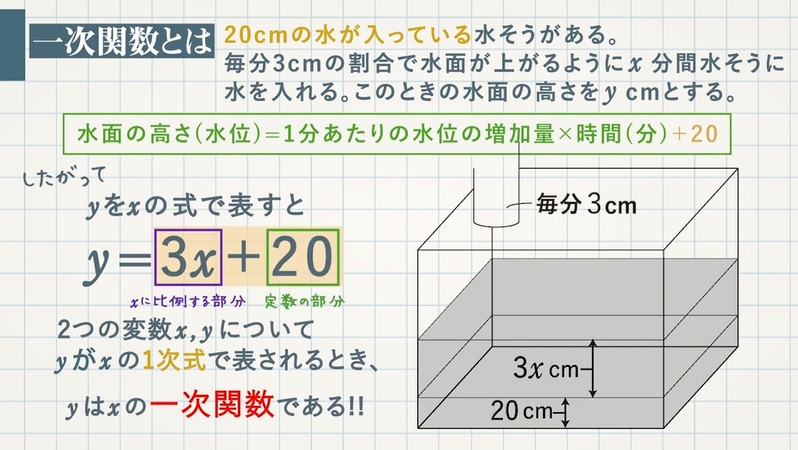
この水そうに $20\rm cm$ の水が入っていて、そこに毎分 $3\rm cm$ の割合で $x$ 分間水を入たときの水面の高さを $y\rm cm$ とすると、水面の高さ(水位) $=$ $1$ 分あたりの水位の増加量 $×$ 時間(分) $\textcolor{blue}{+20}$ となり、$y$ を $x$ の式で表すと、 $\textcolor{blue}{y=3x+20} $ と表すことができます。
$y=3x$ や $y=3x+20$ のように、$2$ つの変数 $x,y$ について、$y$ が $x$ の $1$ 次式で表されるとき、$y$ は $x$ の一次関数であるといいます。