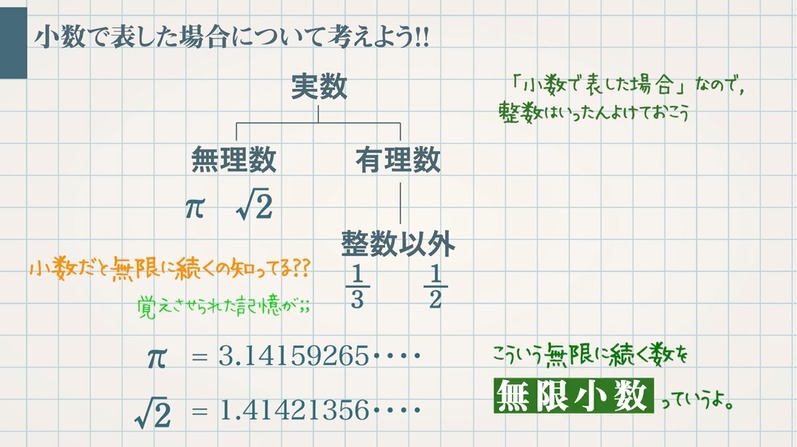
今回は有理数と無理数についてです。

$m$ を整数、$n$ を $0$ でない整数とするとき、分数 $\frac{m}{n}$ で表すことができる数を有理数といいます。

例えば、$3$ は $\frac{3}{1}$ 、$0.3$ は$\frac{3}{10}$ と表すことができるので、$3$ や $0.3$ は有理数です。

これに対して $\sqrt{ 2 }$ や $\sqrt{ 3 }$ はどこまでも続く終わりのない小数なので、分数で表すことができません。このような数を無理数といいます。

また、円周率 $\textcolor{blue}{π}$ も無理数であることがわかっています。

有理数・無理数に分類してみましょう。無理数は $\sqrt{ 　 }$ と円周率 $π$ ですが、分類には注意が必要です。

【例題】次の数を有理数と無理数に分類しなさい。

$ \textcolor{green}{(1) 0}$　　 $\textcolor{green}{(2)0.5　(3)\frac{1}{5}}$

$\textcolor{green}{ (4) π　(5)\sqrt{8}　(6)\sqrt{\frac{1}{4}}}$

無理数→$\sqrt{ 　 }$ と円周率 $π$なので、ふつうに分類すると、(1)～(3)→有理数、(4)～(6)→無理数となりますが、

$(6)\sqrt{\frac{1}{4}}=\sqrt{\frac{1}{2^2}}=\frac{1}{2}$ なので、$\textcolor{red}{\sqrt{\frac{1}{4}}}$ は有理数となります。

円周率 $π$や $\sqrt{2}$ は分数で表すことができないどこまでも続く終わりのない小数でした。

$π=3.14159265　・・・$

$\sqrt{2}=1.41421356　・・・$

このように無限に続く数を無限小数といいます。無限小数は円周率 $π$や $\sqrt{2}$ だけでなく、$\frac{1}{3}$ なども含まれます。

$\frac{1}{3}=1÷3=0.333333　・・・$

無限小数のなかでも $0.333333　・・・$ のように同じ数字が決まった順に繰り返す小数のことを循環小数といい、繰り返す数字の上に点「・」をつけて表します。

【問題】 次の循環小数を分数で表しなさい。

　　　　　$\textcolor{green}{0.\dot{3}}$

① まず、循環小数を $\textcolor{blue}{x}$ とおきます。

② 次に繰り返されるけた数を $\textcolor{blue}{n}$ とし、$x$ を $10^n$ 倍します。（今回は $0.\dot{3}=0.3333　・・・$ なので、繰り返すけた数は１→$10^1$）

\begin{eqnarray} 10x&=&3.3333333・・・\\ -)　　x&=&0.3333333・・・\\ \hline 9x&=&3\\\ x&=&\textcolor{red}{\frac{1}{3}} \end{eqnarray}

【問題】 次の循環小数を分数で表しなさい。

　　　　　$\textcolor{green}{0.\dot{2}\dot{7}}$

① まず、循環小数を $\textcolor{blue}{x}$ とおきます。

② 次に繰り返されるけた数を $\textcolor{blue}{n}$ とし、$x$ を $10^n$ 倍します。

繰り返されるのは、$2$ と $7$ の $\textcolor{blue}{2}$ けたなので、$x$ を $10^\textcolor{blue}{2}$ 倍 ($100$ 倍)

\begin{eqnarray} 100x&=&27.2727272・・・\\ -)　　x&=&\,\,\,0.2727272・・・\\ \hline 99x&=&27\\\ x&=&\textcolor{red}{\frac{3}{11}} \end{eqnarray}