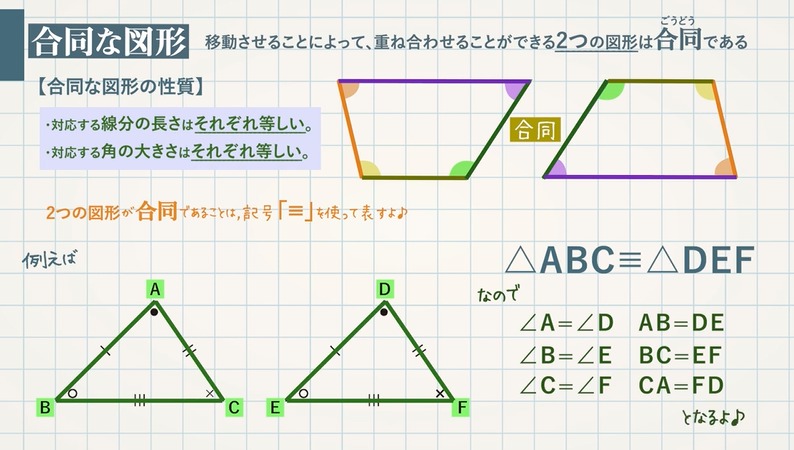
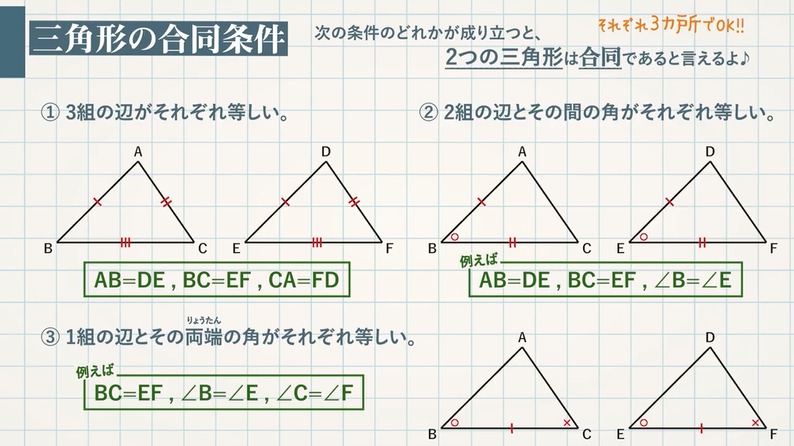
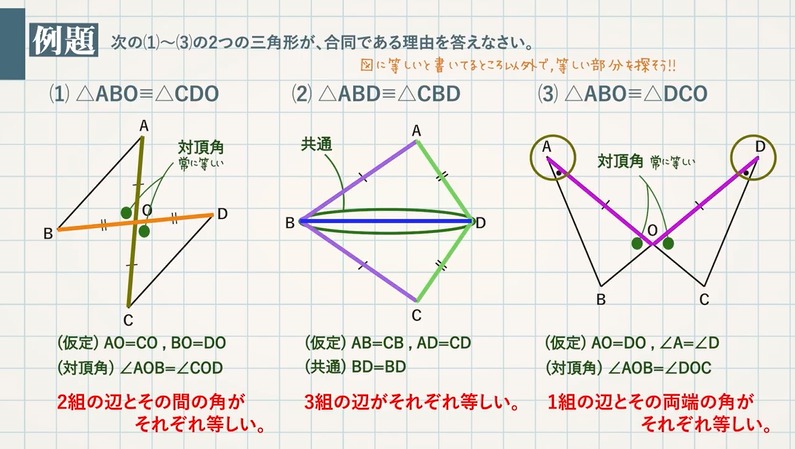
移動させることによって、重ね合わせることができる $2$ つの図形は合同である。
【合同な図形の性質】
・対応する線分の長さはそれぞれ等しい。
・対応する角の大きさはそれぞれ等しい。
$2$ つの図形が合同であることは、記号「≡」を使って表します。
例えば、△ABCと△DEFという$2$ つの三角形が合同であるときは、$\textcolor{blue}{△\rm ABC≡△DEF}$ と表します。
これら $2$ つの三角形は、合同な図形の性質より、
$\textcolor{blue}{∠\rm A=∠D}$ , $\textcolor{blue}{∠\rm B=∠E}$ , $\textcolor{blue}{∠\rm C=∠F}$
$\textcolor{blue}{\rm AB=DE}$ , $\textcolor{blue}{\rm BC=EF}$ , $\textcolor{blue}{\rm CA=FD}$
となります。