まずは角度に関する知識をおさらいしていきましょう。

$1$ . 対頂角・錯角・同位角

対頂角：常に等しい

錯角・同位角：$\textcolor{blue}{2}$ 直線が平行であれば、等しい

$2$ . 内角の和・外角の和

多角形の内角の和：$\textcolor{blue}{180°×(n-2)}$

多角形の外角の和：$\textcolor{blue}{360°}$

以下では、知っている人は得をする裏技をまとめています。各問題の理由の説明は別動画で解説します。

【 Level $\textcolor{green}{1}$ 】次の図で、$\textcolor{green}{∠x}$ の大きさを求めなさい。

(1) POINT：内角 $\textcolor{blue}{+}$ 外角 $\textcolor{blue}{=}$ もう $\textcolor{blue}{1}$ つの外角

よって、$79°+49°=x°$　$x=\textcolor{red}{128°}$

(2) POINT：和（合計）が同じ

よって、$x°+29°=75°$　$x=\textcolor{red}{46°}$

(3) POINT：足すだけ

よって、$23°+56°+27°=x°$　$x=\textcolor{red}{106°}$

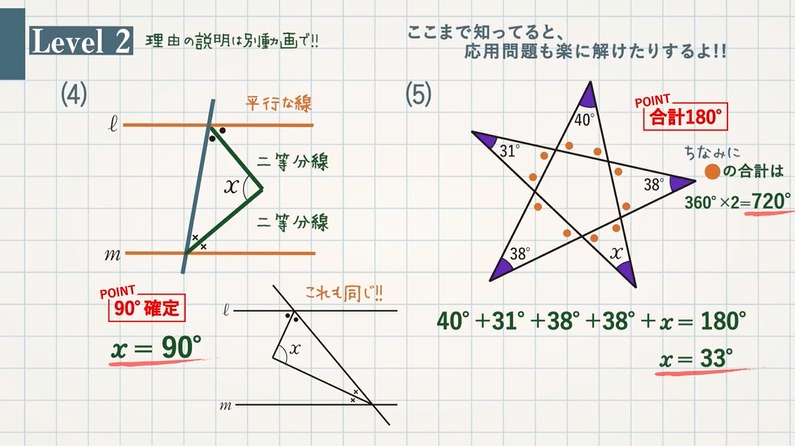
【 Level $\textcolor{green}{2}$ 】次の図で、$\textcolor{green}{∠x}$ の大きさを求めなさい。

(4) POINT：$\textcolor{blue}{90°}$確定

よって、$\textcolor{red}{x=90°}$

(5) POINT：合計 $\textcolor{blue}{180°}$

よって、$40°+31°+38°+38°+x°=180°$

$x=\textcolor{red}{33°}$

ちなみに、オレンジの〇の角度の和は、

$360°×2=\textcolor{red}{720°}$ となります。

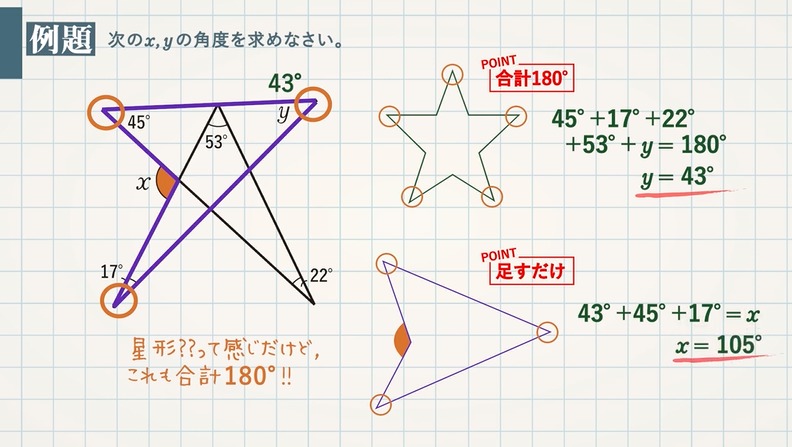
【例題】次の $\textcolor{green}{x,y}$ の角度を求めなさい。

まずは $y$ から求めます。

$\textcolor{green}{y°}$ → POINT：合計 $\textcolor{blue}{180°}$

よって、$45°+17°+22°+53°+y°=180°$　$y=\textcolor{red}{43°}$

次に $x$ を求めます。

$\textcolor{green}{x°}$ →POINT：足すだけ

よって、$43°+45°+17°=x°$　$x=\textcolor{red}{105°}$

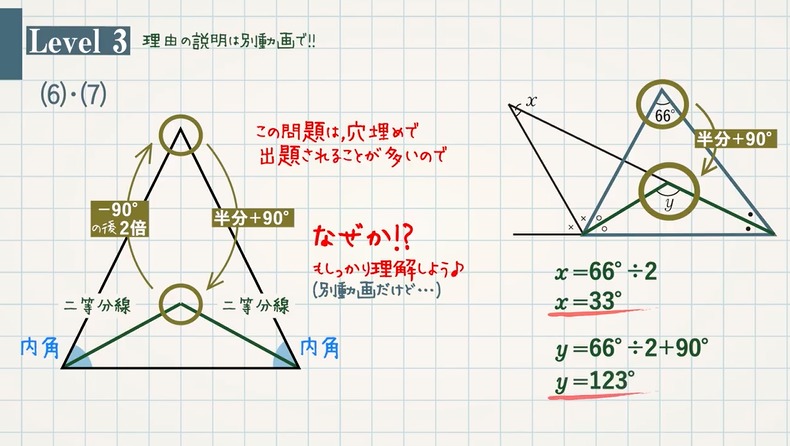
【 Level $\textcolor{green}{3}$ 】次の $\textcolor{green}{x,y}$ の角度を求めなさい。

(6) $\textcolor{green}{x°}$ → POINT：半分に

よって、$x=66°÷2=\textcolor{red}{33°}$

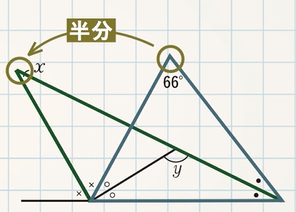
(7) $\textcolor{green}{y°}$ → POINT：半分$\textcolor{blue}{+90°}$に

よって、$y=66°÷2+90°=\textcolor{red}{123°}$