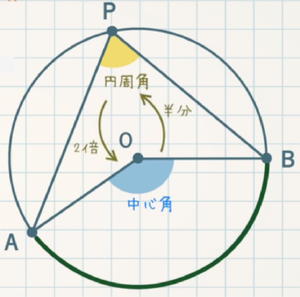
$\stackrel{\frown}{\rm AB}$ の両端 $\rm A, B$ から円周上の点($\rm P$) を結んでできる $\rm ∠APB$ を$\textcolor{blue}{\stackrel{\frown}{\rm AB}}$ の円周角といいます。また、$\rm ∠AOB$ は中心角といいます。(おうぎ形の復習)
円周角の定理はたったの $2$ つだけです。簡単なので、しっかり確認しましょう。
定理 $\textcolor{blue}{1}$ :$\textcolor{blue}{1}$ つの弧に対する円周角は中心角の半分
定理 $\textcolor{blue}{2}$ :$\textcolor{blue}{1}$ つの弧に対する円周角はすべて等しい
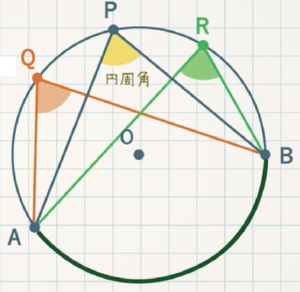
$\rm ∠AQB=∠APB=∠ARB$ (すべて $\stackrel{\frown}{\rm AB}$ に対する円周角)