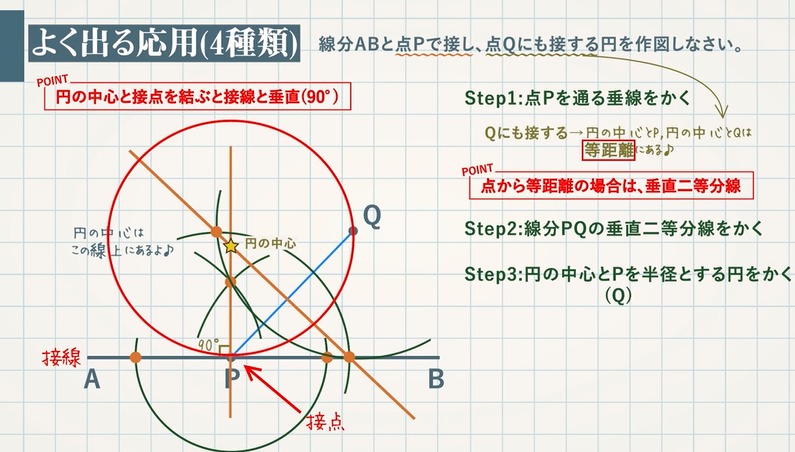
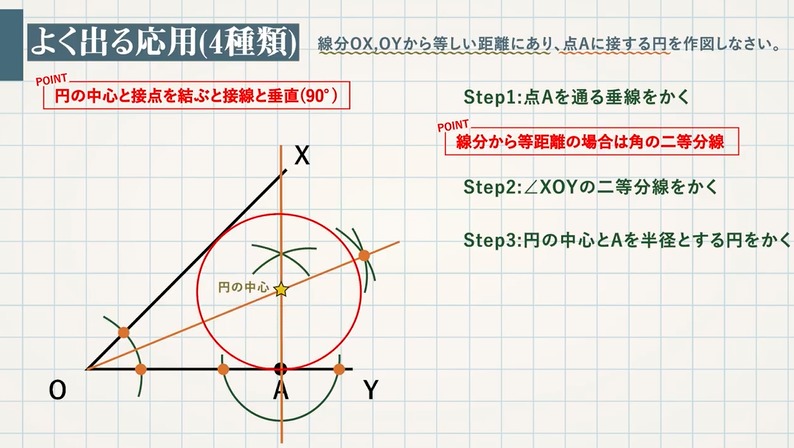
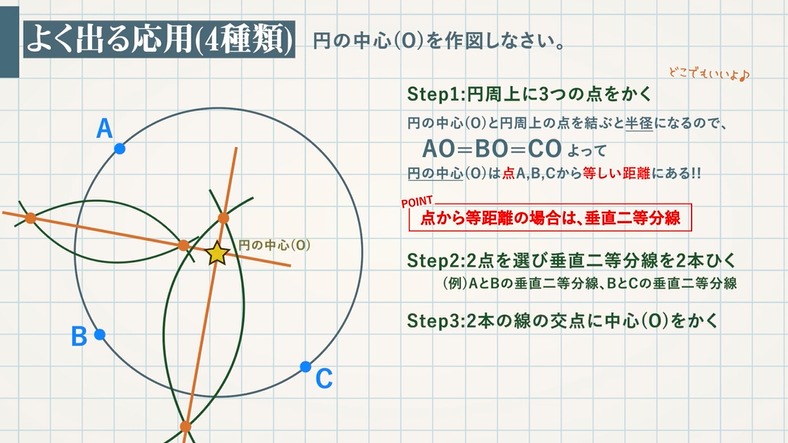
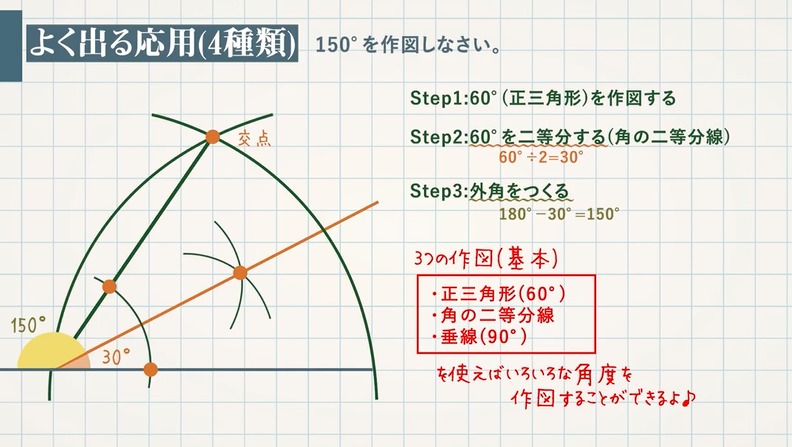
【例題】垂直二等分線を作図しなさい。

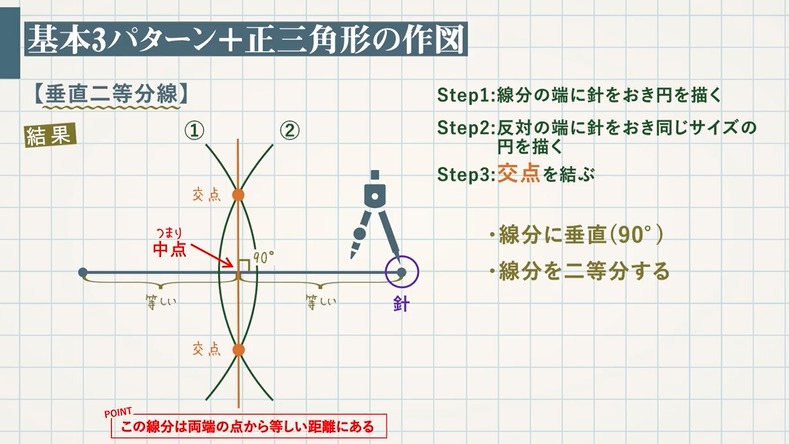
$\textcolor{blue}{\rm Step1}$：線分の端にコンパスの針をおき、円を描く

$\textcolor{blue}{\rm Step2}$：反対の端にコンパスの針をおき、同じサイズの円を描く（コンパスの開きを変えない）

$\textcolor{blue}{\rm Step3}$：交点を結ぶ

垂直二等分線の作図

・線分に垂直（$\textcolor{blue}{90°}$）

・線分を二等分する

線分の垂直二等分線は、その線分の対称の軸といえます。つまり中点を求めたいときにも使えます。

$\textcolor{blue}{\rm POINT}$：この線分は両端の点から等しい距離にある

【例題】角の二等分線を作図しなさい。

$\textcolor{blue}{\rm Step1}$：二等分したい角の頂点にコンパスの針をおき、円を描く

$\textcolor{blue}{\rm Step2}$：交点 $\textcolor{blue}{a}$ にコンパスの針をおき円を描く

$\textcolor{blue}{\rm Step3}$：交点 $\textcolor{blue}{b}$ にコンパスの針をおき同じサイズの円を描く（コンパスの開きを変えない）

$\textcolor{blue}{\rm Step4}$：②と③の交点 $\textcolor{blue}{x}$ と頂点を結ぶ

角の二等分線の作図

・角が二等分される

$\textcolor{blue}{\rm POINT}$：二等分線は角をつくる $\textcolor{blue}{2}$ 辺から等しい距離にある

【例題】点を通る垂線を作図しなさい。

$\textcolor{blue}{\rm Step1}$：点にコンパスの針をおき、線分を通る円を描く

$\textcolor{blue}{\rm Step2}$：交点 $\textcolor{blue}{a}$ にコンパス針をおき円を描く

$\textcolor{blue}{\rm Step3}$：交点 $\textcolor{blue}{b}$ にコンパスの針をおき同じサイズの円を描く（コンパスの開きを変えない）

$\textcolor{blue}{\rm Step4}$：②と③の交点 $\textcolor{blue}{x}$ と頂点を結ぶ

ある点を通る垂線の作図

・点を通り線分に垂直（$\textcolor{blue}{90°}$）

【例題】正三角形を作図しなさい。

$\textcolor{blue}{\rm Step1}$：一本の線をひく

$\textcolor{blue}{\rm Step2}$：線分の端にコンパスの針をおき、線分を半径とする円を描く（コンパスの開きを線分の長さにあわせる）

$\textcolor{blue}{\rm Step3}$：反対の端にコンパスの針をおき、線分を半径とする円を描く（コンパスの開きを変えない）

$\textcolor{blue}{\rm Step4}$：交点と線分の端を結ぶ

正三角形の作図

・すべての辺は等しい

・すべての角は等しい（$\textcolor{blue}{60°}$）

【例題】線分 $\textcolor{green}{\rm AB}$ と点 $\textcolor{green}{\rm P}$ で接し、点 $\textcolor{green}{\rm Q}$ にも接する円を作図しなさい。

$\textcolor{blue}{\rm POINT}$：円の中心と接点を結ぶと接線と垂直（$\textcolor{blue}{90°}$）

$\textcolor{blue}{\rm Step1}$：点 $\textcolor{blue}{\rm P}$ を通る垂線をかく

※円の中心はこの直線上にあります

円は点 $\rm Q$ にも接することから、円の中心と点 $\rm P$、点 $\rm Q$ は等距離にあることがわかります。（どちらも円の半径）

$\textcolor{blue}{\rm POINT}$：点から等距離の場合は、垂直二等分線

$\textcolor{blue}{\rm Step2}$：線分 $\textcolor{blue}{\rm PQ}$ の垂直二等分線をかく

$\textcolor{blue}{\rm Step3}$：円の中心と点 $\textcolor{blue}{\rm P(Q)}$ を半径とする円を描く

【例題】線分 $\textcolor{green}{\rm OX,OY}$ から等しい距離にあり、点 $\textcolor{green}{\rm A}$ に接する円を作図しなさい。

$\textcolor{blue}{\rm POINT}$：円の中心と接点を結ぶと接線と垂直（$\textcolor{blue}{90°}$）

$\textcolor{blue}{\rm Step1}$：点 $\textcolor{blue}{\rm A}$ を通る垂線をかく

※円の中心はこの直線上にあります

問題文より、線分 $\rm OX,OY$ から等しい距離にある

$\textcolor{blue}{\rm POINT}$：線分から等距離の場合は角の二等分線

$\textcolor{blue}{\rm Step2}$：$\textcolor{blue}{\rm ∠XOY}$ の二等分線をかく

$\textcolor{blue}{\rm Step3}$：円の中心と $\textcolor{blue}{\rm A}$ を半径とする円を描く

【例題】円の中心 ($\textcolor{green}{\rm O}$) を作図しなさい。

$\textcolor{blue}{\rm Step1}$：円周上に $\textcolor{blue}{3}$ つの点をかく

※ $3$ 点は円周上であれば、どこにとっても大丈夫です。

円の中心 ($\rm O$) と円周上の点を結ぶと半径になるので、$\textcolor{blue}{\rm AO=BO=CO}$（円の中心 ($\rm O$) は $3$ 点から等しい距離にある）

$\textcolor{blue}{\rm POINT}$：点から等距離の場合は、垂直二等分線

$\textcolor{blue}{\rm Step2}$：$\textcolor{blue}{2}$ 点を選び垂直二等分線を $\textcolor{blue}{2}$ 本ひく

(例) $\rm A$ と $\rm B$ の垂直二等分線、$\rm B$ と $\rm C$ の垂直二等分線

$\textcolor{blue}{\rm Step3}$：$\textcolor{blue}{2}$ 本の線の交点の中心($\textcolor{blue}{\rm O}$) を描く

【例題】$\textcolor{green}{3}$ 点から等しい距離にある点を作図しなさい。 

という問題でも、同じ作図方法になります。

【例題】$150°$ を作図しなさい。

$\textcolor{blue}{\rm Step1}$：$\textcolor{blue}{60°}$ (正三角形を作図する)

$\textcolor{blue}{\rm Step2}$：$\textcolor{blue}{60°}$ を二等分する(角の二等分線)

$60°÷2=30°$

$\textcolor{blue}{\rm Step3}$：外角をつくる

$180°-30°=150°$

基本 $3$ パターンの作図

・正三角形($\textcolor{blue}{60°}$)

・角の二等分線

・垂線($\textcolor{blue}{90°}$) 

を使えばいろいろな角度（$45°,135°$ など) を作図することができます。