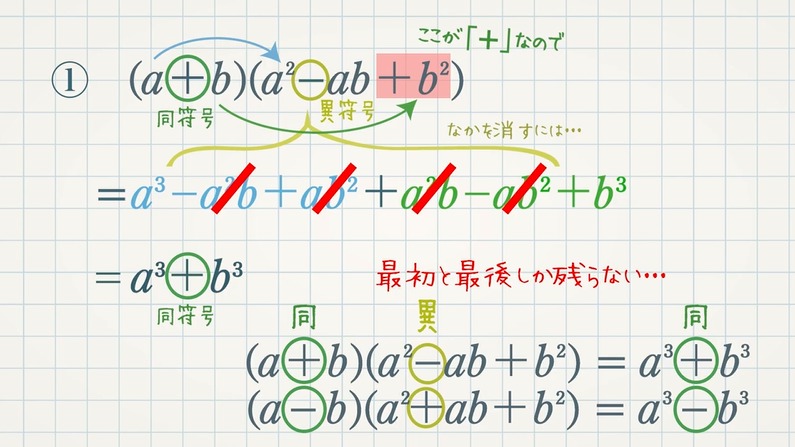
高校で追加される $3$ 次式の公式は、下の $2$ つになります。※符号の違いはあります。

① $\textcolor{blue}{(a+b)(a^2-ab+b^2)=a^3+b^3}$

　　$\textcolor{blue}{(a-b)(a^2+ab+b^2)=a^3-b^3}$

② $\textcolor{blue}{(a+b)^3=a^3+3ab+3ab^2+b^3}$

　　$\textcolor{blue}{(a-b)^3=a^3-3ab+3ab^2-b^3}$

それでは $1$ つずつ確認していきましょう。

まずは、

$\textcolor{blue}{(a+b)(a^2-ab+b^2)=a^3+b^3}$ , $\textcolor{blue}{(a-b)(a^2+ab+b^2)=a^3-b^3}$ についてです。

$(a+b)(a^2-ab+b^2)$ を $1$ つずつ展開して考えると、

　$(a+b)(a^2-ab+b^2)$

$=a^3-a^2b+ab^2+a^2b-ab²+b^3$

$=\textcolor{blue}{a^3+b^3}$　　※最初と最後しか残らない…

よって、

$(a\textcolor{blue}{+}b)(a^2-ab+b^2)=a^3\textcolor{blue}{+}b^3$

$(a\textcolor{blue}{-}b)(a^2+ab+b^2)=a^3\textcolor{blue}{-}b^3$

続いては、

$\textcolor{blue}{(a+b)^3=a^3+3ab+3ab^2+b^3}$ , $\textcolor{blue}{(a-b)^3=a^3-3ab+3ab^2-b^3}$ についてです。

　 $ (a-b)^3$

$=(a-b)(a^2-2ab+b^2)$

$=a^3-2a^2b+ab^2-a^2b+2ab^2-b^3$

$=a^3\textcolor{blue}{-}3a^2b\textcolor{blue}{+}3ab^2\textcolor{blue}{-}b^3$

符号は $-b$ を何回かけたかで決まります。（奇数回は「$\textcolor{blue}{-}$」）

$b$ , $b^3$ →「$\textcolor{blue}{-}$」　　$b^2$ → 「$\textcolor{blue}{+}$」

※$(a+b)^3$ は $b$ が $+$ なので、すべて $+$ になります。

  $(a+b)^3=a^3\textcolor{blue}{+}3ab\textcolor{blue}{+}3ab^2\textcolor{blue}{+}b^3$

【問題】次の式を展開しなさい。

(1) $\textcolor{green}{(2x+1)(4x^2-2x+1)}$

公式 $\textcolor{blue}{(a+b)(a^2-ab+b^2)=a^3+b^3}$ より、

　$=(2x)^3+1^3$

　$=\textcolor{red}{8x^3+1}$

(2) $\textcolor{green}{(3x-2y)^3}$ 

公式 $\textcolor{blue}{(a-b)^3=a^3-3ab+3ab^2-b^3}$ より、

$　=(3x)^3-3×(3x)^2×(2y)+3×3x×(2y)^2-(2y)^3$

　$=\textcolor{red}{27x^3-54x^2y+36xy^2-8y^3}$

因数分解についても問題で確認しておきましょう。

【問題】次の式を因数分解しなさい。

(1) $\textcolor{green}{125x^3-8}$　　

　$=(5x)^3-2^3$　　$a^3-b^3=(a-b)(a^2+ab+b^2)$ より、

$　=\textcolor{red}{(5x-2)(25x^2+10x+4)}$

(2) $\textcolor{green}{a^3+6a^2b+12ab^2+8b^3}$　　

　　$a^3+3ab+3b^2+b^3=(a+b)^3$ より、

　$=\textcolor{red}{(a+2b)^3}$