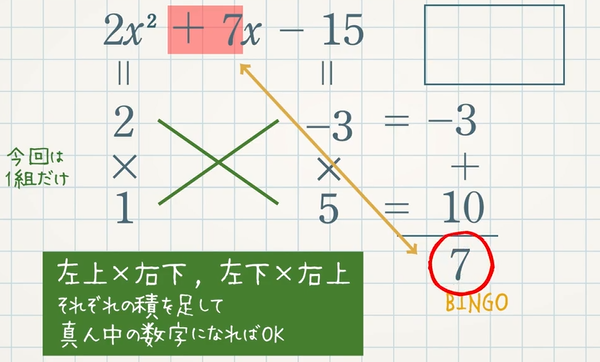
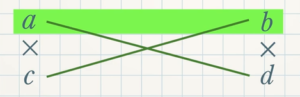
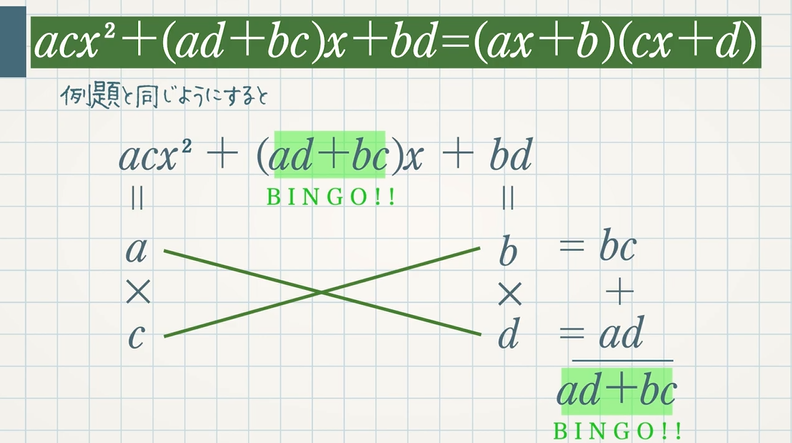$2x^2+7x-15$ のように $x^2$ の係数が $1$ ではない式を因数分解するときに使うのがたすき掛けになります。

$2x^2+7x-15$ を因数分解するとき、

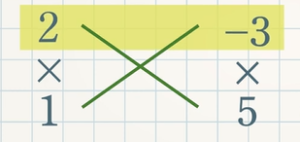
まずは、①かけて $\textcolor{blue}{x^2}$ の係数 $\textcolor{blue}{2}$ になる数字の組み合わせを考えます。

今回は $2×1$ の $1$ 組となります。（ここでは「－」は考えません）

次に、②かけて定数項 $\textcolor{blue}{-15}$ になる数字の組み合わせを考えます。

今回は、$1×-15$ , $-1×15$ , $3×-5$ , $-3×5$ の $4$ つとなります。 

先ほどの $x^2$ の係数の積の組み合わせと、定数項の積の組み合わせを斜めにかけてたしたものが $\textcolor{blue}{x}$ の係数 $\textcolor{blue}{(+7)}$ になるものを考えます。

$2×5=\textcolor{blue}{10}$　,　$1×-3=\textcolor{blue}{-3}$　

$→10-3=\textcolor{blue}{7}$　($x$ の係数 )

それぞれとなりどうしがペアになります。

$\textcolor{blue}{(2x-3)(x+5)}$

$\textcolor{blue}{公式　acx^2+(ad+bc)x+bd=(ax+b)(cx+d)}$

$acx^2+(ad+bc)x+bd$ を因数分解すると、

$x^2$ の係数→ $a×c$　　定数項→$b×d$

これらを斜めにかけてたすと、$b×c+a×d=ad+bc$

それぞれとなりどうしがペアになるので、

$\textcolor{red}{(ax+b)(cx+d)}$

【問題】次の式を因数分解しなさい。

(1) $\textcolor{green}{3x^2-2x-8}$

斜めにかけてたしたものが $x$ の係数 $\textcolor{blue}{-2}$ になる組み合わせ

$1×4=4$　,　$3×(-2)=-6$

その和は、 $4+(-6)=\textcolor{blue}{-2} 　x$の係数

となりどうしがペアとなるので、 $\textcolor{red}{(3x+4)(x-2)}$

(2) $\textcolor{green}{8x^2+14xy-15y^2}$

斜めにかけてたしたものが $xy$ の係数 $\textcolor{blue}{+14}$ になる組み合わせ

$2×(-3)=-6$　,　$4×5=20$

その和は、 $-6+20=\textcolor{blue}{14} 　x$の係数

となりどうしがペアとなるので、$\textcolor{red}{(4x-3y)(2x+5y)}$