数量の等しい関係を文字式を使って表してみましょう。
重さが $a\rm g$ のキャンディー $3$ つと、重さ $b\rm g$ のチョコレート $1$ つで $60\rm g$ になりました。
これを式に表すと、$\textcolor{blue}{3a+b=60}$ となります。
このように、数量の等しい関係を等号($\textcolor{blue}=$)を使って表した式を等式といいます。等式では、等号の左側にある式を左辺、右側にある式を右辺、両方を合わせて両辺といいます。

数量の等しい関係を文字式を使って表してみましょう。
重さが $a\rm g$ のキャンディー $3$ つと、重さ $b\rm g$ のチョコレート $1$ つで $60\rm g$ になりました。
これを式に表すと、$\textcolor{blue}{3a+b=60}$ となります。
このように、数量の等しい関係を等号($\textcolor{blue}=$)を使って表した式を等式といいます。等式では、等号の左側にある式を左辺、右側にある式を右辺、両方を合わせて両辺といいます。

次は数量の大小関係を文字式を使って表しましょう。
重さが $5\rm g$ の封筒に、$1$ 枚 $4\rm g$ の便せんを $a$ 枚入れると $50\rm g$ 以下となった。
これを式に表すと、$\textcolor{blue}{4a+5≦50}$ となります。
このように、数量の大小関係を不等号(≦、<)を使った式を不等式といいます。不等式も等式と同じように、不等式の左側にある式を左辺、右側にある式を右辺、両方を合わせて両辺といいます。
【問題】次の数量の関係を、等式または不等式で表しなさい。
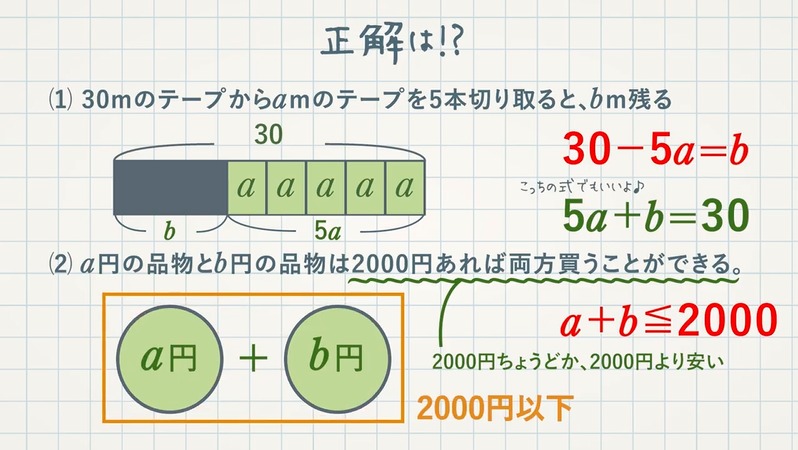
(1) $\textcolor{green}{30\rm m}$ のテープから $\textcolor{green}{a\rm m}$ のテープを $\textcolor{green}{5}$ 本切り取ると、$\textcolor{green}{b\rm m}$ 残る。
$\textcolor{red}{30-5a=b}$ もしくは、$\textcolor{red}{5a+b=30}$
(2) $\textcolor{green}{a}$ 円の品物と $\textcolor{green}{b}$ 円の品物は $\textcolor{green}{2000}$ 円あれば両方買うことができる。
→$\textcolor{blue}{2000}$ 円ちょうどか、$\textcolor{blue}{2000}$ 円より安いということ。
よって、$\textcolor{red}{a+b≦2000}$
コンテンツやシステムに関するお問い合わせ・オファーはこちらから