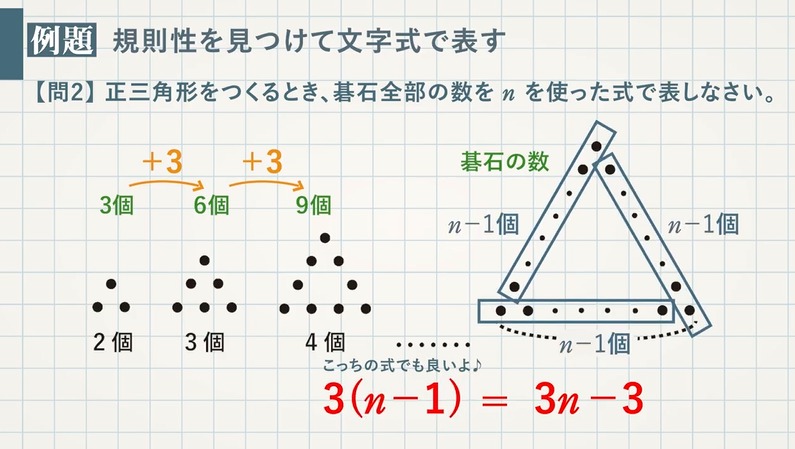
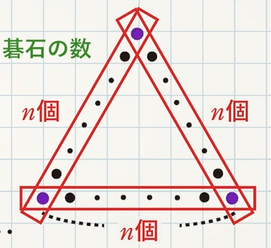
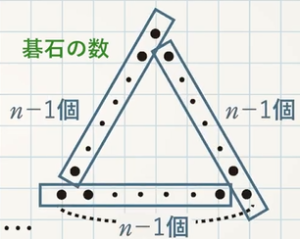
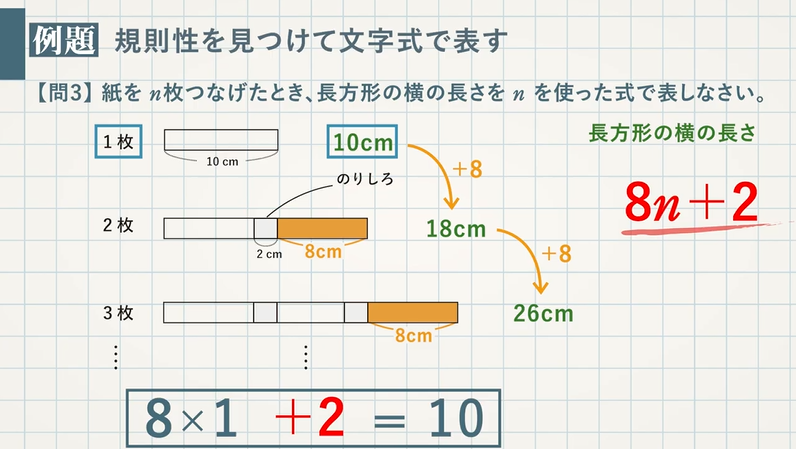
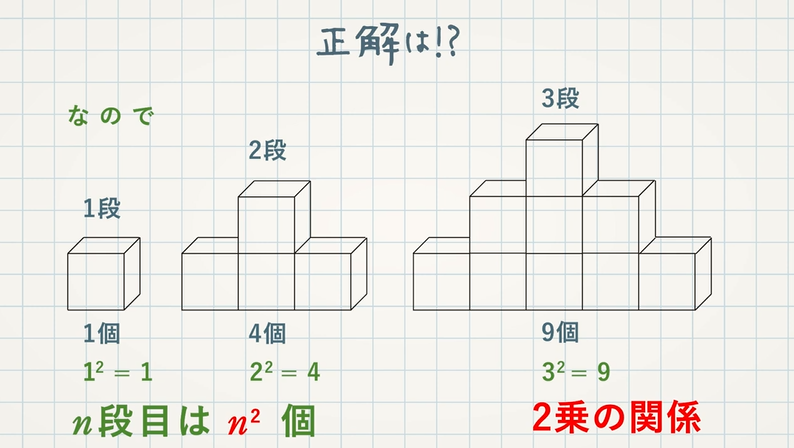
図や文字式を使って、規則性を表してみましょう。

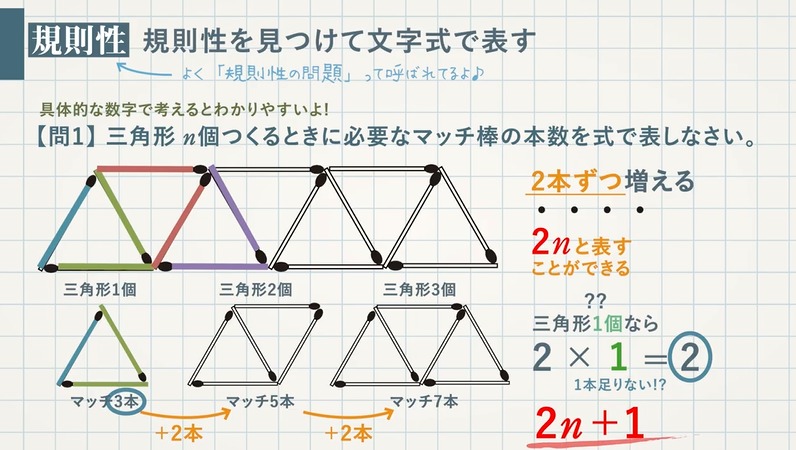
【問 $\textcolor{green}{1}$ 】三角形 $\textcolor{green}{n}$ 個つくるときに必要なマッチ棒の本数を式で表しなさい。

マッチ棒の数は $\textcolor{blue}{2}$ 本ずつ増えている → $\textcolor{blue}{2n}$ と表すことができます。

マッチ棒は $2$ 本ずつ増えていきますが、初めの１本を加えないと必要なマッチ棒の本数を表すことができません。

よって、必要なマッチ棒の本数を式で表すと $\textcolor{red}{2n+1}$ となります。

規則性を文字式で表すことができると、数えなくても色々なことがわかります。

① 三角形を $\textcolor{green}{7}$ 個つくるときに必要なマッチ棒の本数は？

$\textcolor{blue}{2n+1}$ に $n=7$ を代入

$2×7+1=15$　

よって、必要なマッチ棒の本数は $\textcolor{red}{15}$ 本

② マッチ棒 $\textcolor{green}{101}$ 本でつくることのできる三角形の個数は？

$\textcolor{blue}{2n+1}=101$　より、$n=50$

よって、できる三角形の個数は $\textcolor{red}{50}$ 個

【問 $\textcolor{green}{2}$】 正三角形をつくるとき、碁石全部の数を $\textcolor{green}{n}$ を使った式で表しなさい。

碁石の数は $\textcolor{blue}{3}$ 個ずつ増えているので、$\textcolor{blue}{3n}$

$1$ 辺 $n$ 個とすると、重なる部分が $3$ つあるので、$\textcolor{red}{3n-3}$　(画像赤)

または、$1$ 辺が $n-1$ 個なので $\textcolor{red}{3(n-1)}$　(画像青)

【問 $\textcolor{green}{3}$ 】  紙を $\textcolor{green}{n}$ 枚つなげたとき、長方形の横の長さを $\textcolor{green}{n}$ を使った式で表しなさい。

長方形の横の長さは $\textcolor{blue}{8 \rm cm}$ ずつ増えているので、

　→　$\textcolor{blue}{8n}$

重ならない紙（のりしろ部分がない） が必ず $1$ つあるので、

　→　$\textcolor{red}{8n+2}$

【問 $\textcolor{green}{4}$ 】 立方体を $\textcolor{green}{n}$ 段重ねるのに必要な立方体の個数を $\textcolor{green}{n}$ を使った式で表しなさい。

立方体の個数は、$1$ 段で $1$ 個、$2$ 段で $4$ 個、$3$ 段で $9$ 個 となります。

このことから、段数と立方体の個数には$\textcolor{blue}{2}$ 乗の関係があることがわかります。

$1$ 段　→　$1^2$個 　　$2$ 段　→　$2^2$個　　$3$ 段　→　$3^2$個

よって、$n$ 段目の立方体の個数は $\textcolor{red}{n^2}$ 個 となります。