PDF教材

ダウンロード

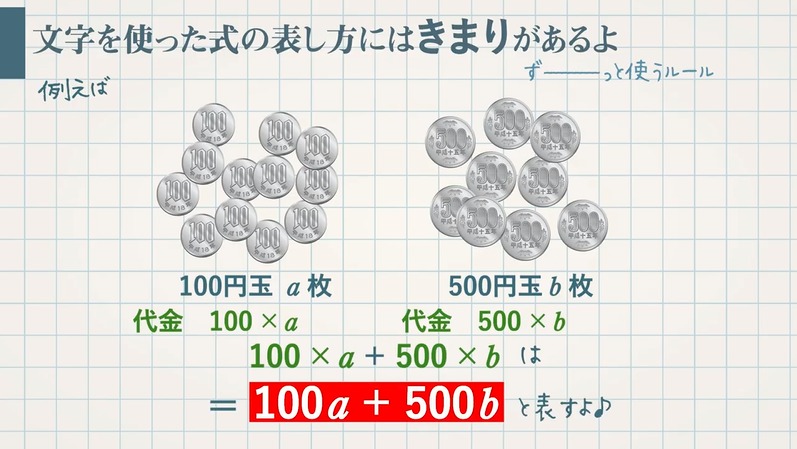
文字式での表し方には決まった表し方があります。

例えば、$100$ 円玉 $a$ 枚と $500$ 玉 $b$ 枚の金額の合計はというと、

$100$ 円玉が $a$ 枚なので、$100×a$ 円

$500$ 円玉が $b$ 枚なので、$500×b$ 円

よって、合計金額は $100×a+500×b=\textcolor{blue}{100a+500b}$ と表します。どういった決まりがあるのか、みていきましょう。

まずは、文字式の表し方の $4$ つの基本ルールを確認しましょう。

① 文字の混じったかけ算では、「$\textcolor{blue}{×}$」をはぶく

　例　$a×b×c=\textcolor{blue}{abc}$

② 文字と数の積（かけ算）では、数を前にかく

　例　$a×2=\textcolor{blue}{2a}$

③ 同じ文字の積は、累乗を使う

　例　$x×x×x×y×y=\textcolor{blue}{x^3y^2}$

④ わり算では、「÷」を使わず、分数の形でかく

　例　$a÷b=\textcolor{blue}{\frac{a}{b}}$

基本ルール以外の細かなルールを問題で確認していきましょう。

【問題】次の計算をしなさい。

\begin{eqnarray} \textcolor{green}{(1)}&　&\textcolor{green}{x×(-1)}=-1x=\textcolor{red}{-x}\\ &　&\textcolor{blue}{1 は省略}\\\\ \textcolor{green}{(2)}&　&\textcolor{green}{a×2×b×a}=\textcolor{red}{2a^2b}\\ &　&\textcolor{blue}{文字はアルファベット順}\\\\ \textcolor{green}{(3)}&　&\textcolor{green}{a÷(-2)}=\frac{a}{-2}=\textcolor{red}{-\frac{a}{2}}\\ &　&\textcolor{blue}{分母・分子の「-」は分数の前に}\\\\ \textcolor{green}{(4)}&　&\textcolor{green}{(x+3)÷4}=\frac{(x+3)}{4}=\textcolor{red}{\frac{x+3}{4}}\\ &　&\textcolor{blue}{分数のかっこは基本省略}\\\\ \end{eqnarray}

\begin{eqnarray}\textcolor{green}{(5)}&　&\textcolor{green}{a÷b×c÷d}\\ &　&\textcolor{blue}{除法は、乗法になおして計算（逆数にしてかける）}\\ & &=a×\frac{1}{b}×c×\frac{1}{d}=\textcolor{red}{\frac{ac}{bd}} \\\\\\ \textcolor{green}{(6)}&　&\textcolor{green}{2×(n+1)-b÷c}\\ &　&\textcolor{blue}{「+」「-」は省略できないので、前後にわける}\\ & &=2(n+1)-b×\frac{1}{c}=\textcolor{red}{2(n+1)-\frac{b}{c}} \end{eqnarray}