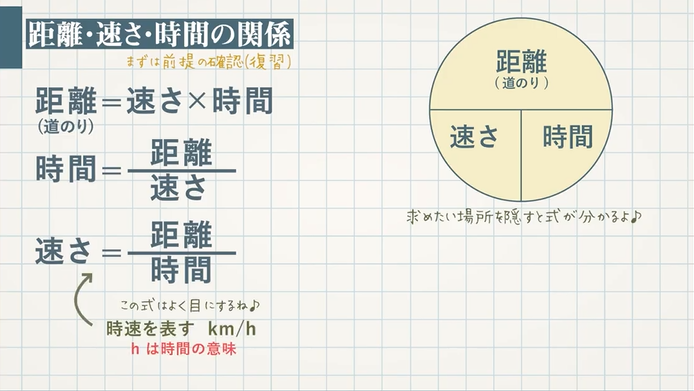
まずは復習として距離・速さ・時間の関係を復習しておきましょう。

\begin{eqnarray} 距離　&=&　速さ × 時間\newline\\ 時間　&=&　\frac{距離}{速さ}\newline\\ 速さ　&=&　\frac{距離}{時間}\newline\\ \end{eqnarray}

これらを関係を使う文章題にチャレンジしましょう。

【例題①】池のまわりに $\textcolor{green}{1}$ 周 $\textcolor{green}{3000\rm m}$ の遊歩道がある。A,Bが同じ地点から互いに反対方向にスタートし、Aは分速 $\textcolor{green}{80\rm m}$ で歩き、Bは分速 $\textcolor{green}{170\rm m}$ で走ったとき、何分後に $\textcolor{green}{2}$ 人が出会うか求めなさい。

STEP１：どの数量を文字を使って表すのか決める

$2$ 人が出会うまでにかかる時間(分)を $x$ とする。

STEP２：等しい数量の関係をみつけ、方程式をつくる

Aの歩いた距離 $+$ Bの走った距離 $=$ 池の周りの距離 より、$\textcolor{blue}{80x+170x=3000}$

STEP３：方程式の解を求める

$80x+170x=3000$

　　　　　$\textcolor{blue}{x=12}$

STEP４：問題に適しているか確かめる

$2$ 人が出発して $12$ 分後に出会うは問題に適している。

よって、$\textcolor{red}{2}$ 人が出発して $\textcolor{red}{12}$ 分後に出会う

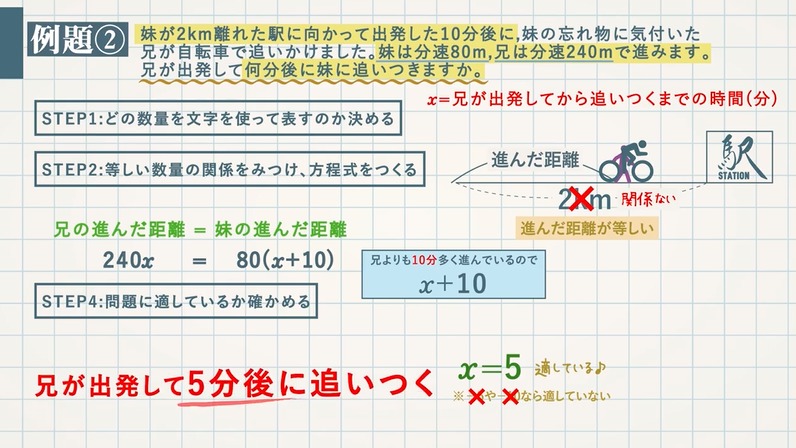
【例題②】妹が $\textcolor{green}{2\rm km}$ 離れた駅に向かって出発した $\textcolor{green}{10}$ 分後に、妹の忘れ物に気付いた兄が自転車で追いかけました。妹は分速 $\textcolor{green}{80\rm m}$ 、兄は分速 $\textcolor{green}{240\rm m}$ で進みます。兄が出発して何分後に妹に追いつきますか。

STEP１：どの数量を文字を使って表すのか決める

兄が出発してから追いつくまでの時間を $x$ とする。

STEP２：等しい数量の関係をみつけ、方程式をつくる

兄の進んだ距離 $=$ 妹の進んだ距離 より、$\textcolor{blue}{240x=80(x+10)}$

STEP３：方程式の解を求める

$240x=80(x+10)$

　   $\textcolor{blue}{x=5}$

STEP４：問題に適しているか確かめる

兄が出発して $5$ 分後に追いつくは問題に適している。

よって、兄が出発して $\textcolor{red}{5}$ 分後に出会う

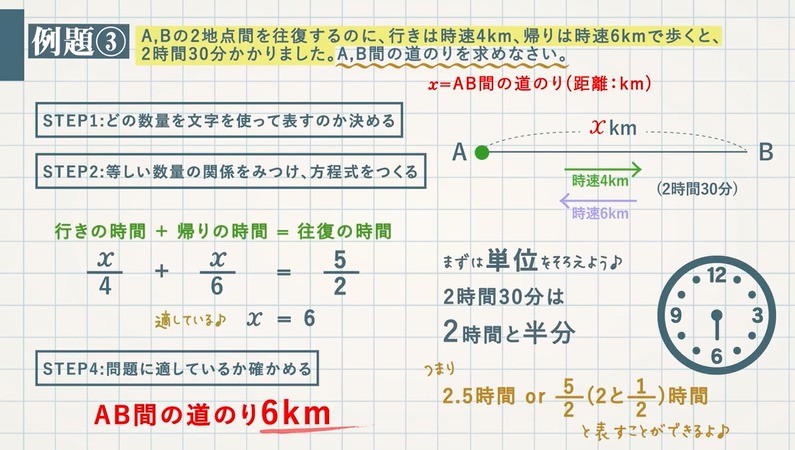
【例題③】A,Bの $\textcolor{green}{2}$ 地点間を往復するのに、行きは時速 $\textcolor{green}{4\rm km}$ 、帰りは時速 $\textcolor{green}{6\rm km}$ で歩くと、$\textcolor{green}{2}$ 時間 $\textcolor{green}{30}$ 分かかりました。A,B間の道のりを求めなさい。

STEP１：どの数量を文字を使って表すのか決める

A,B間の道のりを $x$ とする。

STEP２：等しい数量の関係をみつけ、方程式をつくる

行きの時間 $+$ 帰りの時間 $=$ 往復の時間 より、 \begin{eqnarray}\textcolor{blue}{\frac{x}{4}+\frac{x}{6}}&\textcolor{blue}{=}&\textcolor{blue}{\frac{5}{2}}\\ \end{eqnarray}

STEP３：方程式の解を求める

\begin{eqnarray} \frac{x}{4}+\frac{x}{6}&=&\frac{5}{2}\\\textcolor{blue}{x}&\textcolor{blue}{=}&\textcolor{blue}{6}\\ \end{eqnarray}

STEP４：問題に適しているか確かめる

A,B間の道のりが $6\rm km$ は問題に適している。

よって、A,B間の道のり $\textcolor{red}{6\rm km}$