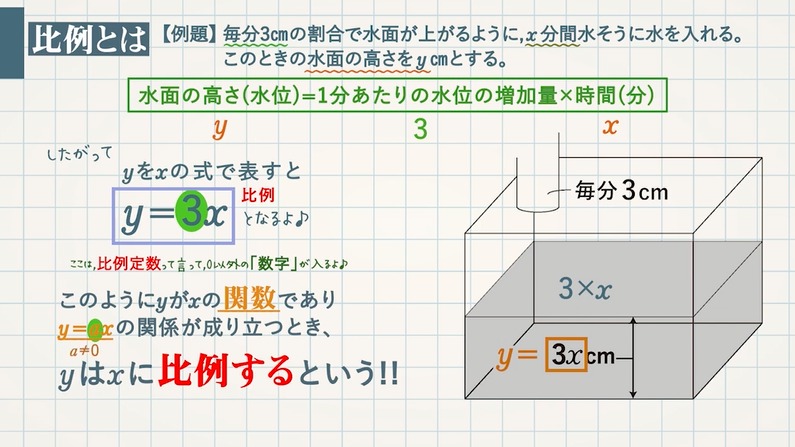
【例題】毎分 $\textcolor{green}{3\rm cm}$ の割合で水面が上がるように、$\textcolor{green}{x}$ 分間水そうに水を入れる。このときの水面の高さを $\textcolor{green}{y\rm cm}$ とする。

水面の高さ(水位) $=$ $1$ 分あたりの水位の増加量 $×$ 時間(分)

 　   　  $y$　 　 　 $=$　　　　   　$3$　　　　　　$×$　 $x$

したがって、$y$ を $x$ の式で表すと、$\textcolor{red}{y=3x}$ となります。

$\textcolor{blue}{3}$ の部分を比例定数といい、$0$ の以外の数字が入ります。 

このように $y$ が $x$ の関数であり、$\textcolor{blue}{y=ax（a≠0）}$ の関係が成り立つとき、$y$ は $x$ に比例するといいます。

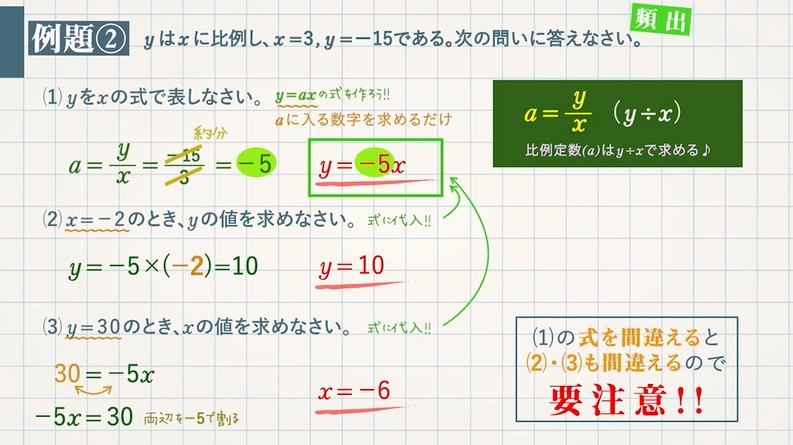
比例定数 ($\textcolor{blue}{a}$) は $1$ 組の $x$ と $y$ の値で求めることができます。

　$\textcolor{blue}{a=\frac{y}{x}}$　$\textcolor{blue}{（y÷x）}$

【例題①】次のア～オの中から、$\textcolor{green}{y}$ が $\textcolor{green}{x}$ に比例するものをすべて選びなさい。

ア　$\textcolor{green}{y=3x}$　　　イ　$\textcolor{green}{y=\frac{8}{x}}$　　　ウ　$\textcolor{green}{y=-2x}$

エ　$\textcolor{green}{y=\frac{x}{8}}$　　　 オ　$\textcolor{green}{y=3+x}$

ア→〇　比例定数 $\textcolor{blue}{3}$

イ→✕　次回習う反比例 ($\textcolor{blue}{y=\frac{a}{x}}$) の形です。

ウ→〇　比例定数 $\textcolor{blue}{-2}$

エ→〇　$y=\frac{x}{8}$ と $y=\frac{1}{8}x$ は同じ意味　比例定数 $\textcolor{blue}{\frac{1}{8}}$

オ→✕　$2$ 年生で習う $\textcolor{blue}{1}$ 次関数 ($\textcolor{blue}{y=ax+b}$) の形です。

【例題②】$\textcolor{green}{y}$ は $\textcolor{green}{x}$ に比例し、$\textcolor{green}{x＝3}$ , $\textcolor{green}{y=-15}$ である。次の問いに答えなさい。

(1)　$\textcolor{green}{y}$ を $\textcolor{green}{x}$ の式で表しなさい。

$y=ax$ の式をつくるには、$a$ に入る数字を求めます。

$a=\frac{y}{x}=\frac{-15}{3}=-5$　 $\textcolor{red}{y=-5x}$

(2)　$\textcolor{green}{x=-2}$ のとき、$\textcolor{green}{y}$ の値を求めなさい。

$y=-5x$ に代入

$y=-5×(\textcolor{blue}{-2})=10　　y=\textcolor{red}{10}$　　

(3)　$\textcolor{green}{y=30}$ のとき、$\textcolor{green}{x}$ の値を求めなさい。

$y=-5x$ に代入

$\textcolor{blue}{30}=-5x$　　これを解いて、$x=\textcolor{red}{-6}$

(1) の式を間違えると、(2)・(3)も間違えてしまうので、注意しましょう。　

【例題③】$\textcolor{green}{1}$ 辺が $\textcolor{green}{x\rm cm}$ の正方形の周の長さを $\textcolor{green}{y\rm cm}$ として、その関係を表に表しなさい。

表を作るときは、$x$ の値を式に代入します。

まずは式をつくりましょう。

正方形なので、$1$ 辺が $x\rm cm$ の辺が $4$ つあります。

よって、周の長さ $y$ は $\textcolor{blue}{y=4x}$ と表すことができます。 

$x$ の値を代入して、対応する $y$ の値を求めましょう。

$y=4×1=\textcolor{red}{4}$　　$y=4×2=\textcolor{red}{8}$　$y=4×3=\textcolor{red}{12}$

$y=4×4=\textcolor{red}{16}$　$y=4×5=\textcolor{red}{20}$

ちなみに、$y$ が $x$ に比例するときは、$\textcolor{blue}{x}$ の値が $\textcolor{blue}{2}$ 倍、$\textcolor{blue}{3}$ 倍・・・ になると、対応する $\textcolor{blue}{y}$ の値も $\textcolor{blue}{2}$ 倍、$\textcolor{blue}{3}$ 倍・・・になります。