【問題】図の円錐の体積を求めなさい。

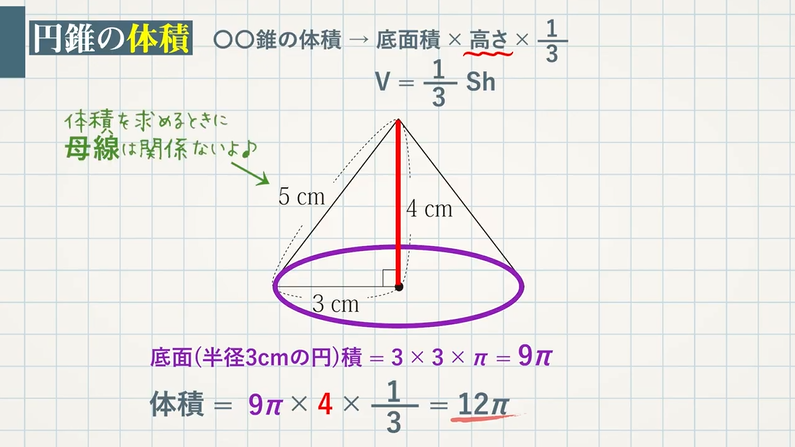
○錐の体積 → $\textcolor{blue}{底面積×高さ×\frac{1}{3}}$　$\textcolor{blue}{\rm {V=\frac{1}{3}S}h}$

円錐の底面は円なので、底面積は$3×3×π=\textcolor{blue}{9π}$　

高さは $\textcolor{blue}{4\rm cm}$ 

よって、体積は $9π × 4 \rm {cm} ×\frac{1}{3}=\textcolor{red}{12π \rm cm^3}$ 

※体積を求めるときに、母線の長さは使いません。

【問題】側面のおうぎ形の弧の長さを求めなさい。

側面のおうぎ形の弧の長さは、底面の円周と同じ長さになります。

半径 $3 \rm cm$ の円なので、$2×3×π=\textcolor{red}{6π\rm cm}$

【問題】側面のおうぎ形の中心角の大きさを求めなさい。

側面のおうぎ形は半径 $5 \rm cm$ の円の一部といえます。よって、円周と弧の長さの比率から、おうぎ形の中心角を求めることができます。

半径 $5 \rm cm$ の円周なので、$2×5×π=\textcolor{blue}{10π}$

側面のおうぎ形の弧の長さは、$\textcolor{blue}{6π}$

\begin{eqnarray} & &おうぎ形は半径 5 \rm {cm} の円の\frac{6π}{10π}=\frac{3}{5}倍\\& &よって、中心角は 360°×\frac{3}{5}=\textcolor{red}{216°}\end{eqnarray}

【問題】側面積を求めなさい。

側面はおうぎ形になるので、

\begin{eqnarray}5^2×π×\frac{216}{360}=\textcolor{red}{15π \rm {cm^2}} 　おうぎ形の面積：\textcolor{blue}{πr^2×\frac{中心角}{360} }\end{eqnarray}

ですが、次の方法で簡単に計算することができます。

円すいの側面積 $\textcolor{blue}{=}$ 母線 $\textcolor{blue}{×}$ 半径 $\textcolor{blue}{×}$ π

$5×3×π=\textcolor{red}{15π \rm cm^2}$

【問題】表面積を求めなさい。

表面積 $\textcolor{blue}{=}$ 側面積 $\textcolor{blue}{+}$ 底面積　

底面積は $9π \rm cm^2$ 、側面積は $15π \rm cm^2$

よって、表面積は  $15π+9π=\textcolor{red}{24π\rm cm^2}$

【問題】図のような円錐を、Oを中心に転がすと、$\textcolor{green}{3}$ 回転してもとの位置に戻りました。円錐の母線の長さを求めなさい。

 $3$ 回転ということは、中心がOである大きい円の円周は、側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さと等しくなります。

おうぎ形の弧の長さは、$2×6×π=12π \rm cm$

大きい円の円周は、$12π×3=36π \rm cm$

母線の長さは、大きい円の半径の長さと同じなので、円周の公式より、

$2×□×π=36π$　

よって、母線の長さは $\textcolor{red}{18 \rm cm}$ となります。