以下のようなテスト結果であったとき、

$52$ 点、$78$ 点、$88$ 点、$63$ 点、$32$ 点

$85$ 点、$69$ 点、$41$ 点、$70$ 点、$92$ 点

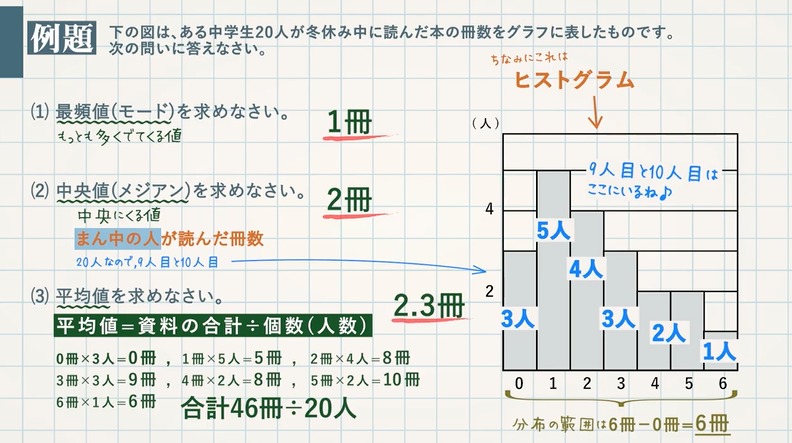
平均値 $\textcolor{blue}{=}$ 資料の合計 $\textcolor{blue}{÷}$ 個数（人数）

$52+78+88+63+32+85+69+41+70+92=670$

$670÷10$　平均点は $\textcolor{blue}{67}$ 点になります。

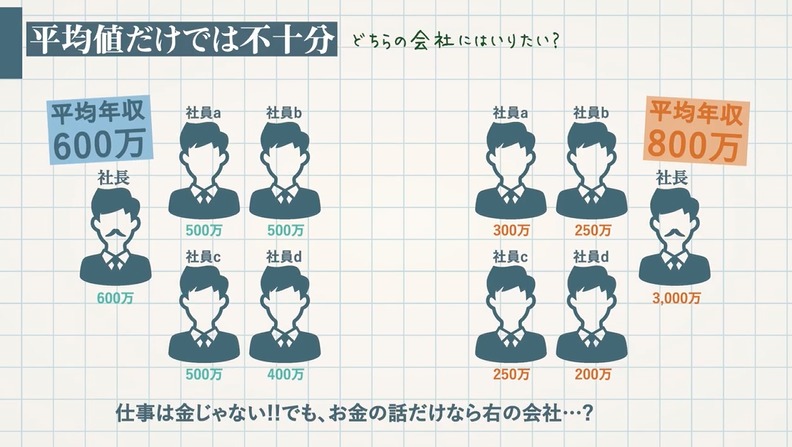
この平均点のように、たくさんある資料を「$\textcolor{blue}{1}$ つの数値で代表させる」ものを代表値といいます。

平均年収 $500$ 万の会社と平均年収 $800$ 万の会社があるとします。お金だけの話なら平均年収 $800$ 万の会社を選ぶ方が良い？

平均年収 $500$ 万の会社の内訳

社長：$600万$

社員a～d：$500$ 万、$500$ 万、$500$ 万、$400$ 万

平均年収 $800$ 万の会社の内訳

社長：$3,000万$

社員a～d：$300$ 万、$250$ 万、$250$ 万、$200$ 万

→平均年収は $800$ 万だけど、社長の給料が多いだけです。

なので、平均値以外の代表値も必要となります。

平均値以外の代表値として、中央値（メジアン）・最頻値（モード）があります。

中央値：資料を大きい順に並べたとき、中央にくる値

今回資料は $5$ つなので、中央は $\textcolor{blue}{3}$ つ目になります。

平均年収 $500$ 万の会社

$600万$、$500$ 万、$\textcolor{blue}{500}$ 万（中央値）、$500$ 万、$400$ 万

平均年収 $800$ 万の会社

$3,000万$、$300$ 万、$\textcolor{blue}{250}$ 万（中央値）、$250$ 万、$200$ 万

最頻値：資料の中で、もっとも多くでてくる値

平均年収 $500$ 万の会社

$600万$、$\textcolor{blue}{500}$ 万、$\textcolor{blue}{500}$ 万、$\textcolor{blue}{500}$ 万、$400$ 万

平均年収 $800$ 万の会社

$3,000万$、$300$ 万、$\textcolor{blue}{250}$ 万、$\textcolor{blue}{250}$ 万、$200$ 万

【例題】図は、ある中学生 $\textcolor{green}{20}$ 人が冬休み中に読んだ本の冊数をグラフに表したものです。次の問いに答えなさい。

図のようなグラフをヒストグラムといいます。

(1) 最頻値(モード)を求めなさい。

もっとも多くでてくる値。一番人数の多い $5$ 人である $\textcolor{red}{1}$ 冊

(2) 中央値(メジアン)を求めなさい。

中央にくる値。

資料の個数は $20$ ( $20$ 人) なので、$9$ 人目と $10$ 人目　$\textcolor{red}{2}$ 冊

(3) 平均値を求めなさい。

　平均値 $\textcolor{blue}{=}$ 資料の合計 $\textcolor{blue}{÷}$ 個数（人数）

資料の合計

$0冊×3人=0冊$、$1冊×5人=5冊$、$2冊×4人=8冊$

$3冊×3人=9冊$、$4冊×2人=8冊$、$5冊×2人=10冊$

$6冊×1人=6冊$

合計 $46$ 冊 $÷$ $20$ 人 $=$ $\textcolor{red}{2.3}$ 冊