日常で使う数字は四捨五入した「だいたい」の値を使うことが多いです。

例えば「ものさしである物体の長さをはかるとき」

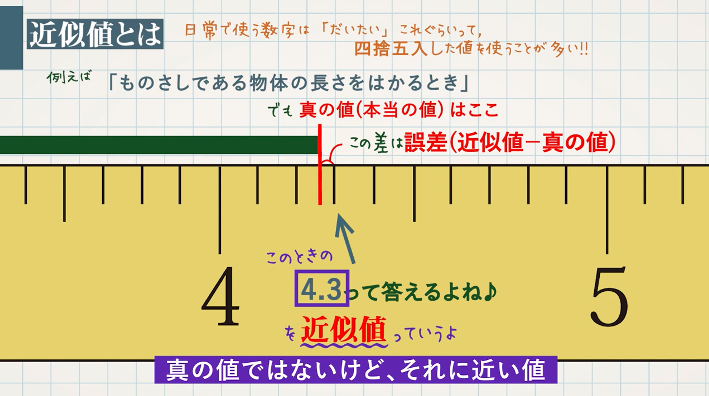
図の緑の長さは $4.3$ と答えますが、真の値（本当の値）は $4.28・・・$ となります。このときの $4.3$ を近似値といいます。

近似値：真の値ではないけど、それに近い値

また、近似値と真の値の差を誤差といいます。

誤差：近似値 $\textcolor{blue}{-}$ 真の値

(1) 近似値が $\textcolor{green}{52}$、真の値が $\textcolor{green}{51.7}$ のとき誤差を求めなさい。

誤差 $\textcolor{blue}{=}$ 近似値 $\textcolor{blue}{-}$ 真の値

$52-51.7=\textcolor{red}{0.3}
$

(2) $\textcolor{green}{1\rm g}$ 未満を四捨五入して重さを量ると $\textcolor{green}{245\rm g}$ であった。真の値を $\textcolor{green}{a\rm g}$ として、$\textcolor{green}{a}$ の値の範囲を不等号を使って表しなさい。

範囲を求めるときは、最大と最小を考えます。

四捨五入して $245$ になる最小の値は、$244.5$。最大の値は、$245.49999・・・$。つまり、$245.5$ の直前の値となります。

よって、$a$ の範囲は $\textcolor{red}{244.5≦a＜245.5}$

(3) $\textcolor{green}{5.3168}$ の小数第 $\textcolor{green}{3}$ 位を四捨五入したときの誤差を求めなさい。

小数第 $3$ 位を四捨五入すると → $5.32$（近似値）

近似値 $\textcolor{blue}{-}$ 真の値なので、$5.32-5.3168=\textcolor{red}{0.0032}$

近似値で示されると、どの数まで信頼して良いのかわからなくなります。例えば、目もりの最小が $10 \rm g$ のはかりで $250 \rm g$ と表示された場合、真の値が $252 \rm g$ でも $254 \rm g$ でも同じように表示されます。この中でも信頼できる数字（今回でいうと $\textcolor{blue}{25}$ の部分）を有効数字といいます。

POINT：近似値のうち、信頼できる数字を有効数字という

【有効数字をはっきり示す方法】

　整数部分が $\textcolor{blue}{1}$ ケタの有限小数 $\textcolor{blue}{×}$ $\textcolor{blue}{10}$ の累乗　　

　整数部分が $\textcolor{blue}{1}$ ケタの有限小数 $\textcolor{blue}{×}$ $\textcolor{blue}{\frac{1}{10 の累乗}}$

有効数字を $3$ ケタとすると、

$5460=5.46×10^3$　$,$　$0.0123=1.23×\frac{1}{10^2}$　

と示すことができます。

(1) 測定値 $\textcolor{green}{1.6×10^4}$ は、何の位まで測定したものか答えなさい。

$1.6×10^4=16000$ → 千の位

(2) $\textcolor{green}{10 \rm cm}$ 未満を四捨五入したところ、$\textcolor{green}{8000\rm cm}$ となった。有効数字を答えなさい。

$10\rm cm$ 未満 → 一の位のことなので、その有効数字は $\textcolor{red}{8,0,0}$　

※「$\textcolor{blue}{0}$」が有効数字の場合もあります。

(3) ある荷物の長さをはかると $\textcolor{green}{3200\rm cm}$ であった。有効数字 $\textcolor{green}{2}$ ケタであるとき、整数部分が $\textcolor{green}{1}$ ケタの小数と $\textcolor{green}{10}$ の累乗の積の形で表しなさい。

有効数字 $2$ ケタなので、$3.2×1000$

よって、$\textcolor{red}{3.2×10^3}$ となります。※累乗は「$\textcolor{blue}{0}$」の数