「速さ」に関する問題を扱うときは、マイナス（負の数）をはぶき、座標平面の右上のみを使います。

グラフのヨコ軸（$x$ 軸）を時間、タテ軸（$y$ 軸）とすると、

傾き（$\textcolor{blue}{a}$）$\textcolor{blue}{=}$ 速さとなります。

\begin{eqnarray} \frac{yの増加量}{xの増加量}=\frac{距離}{時間} \end{eqnarray}

また、傾きがマイナスになる場合は、その絶対値が速さになります。（例）傾き（$a$）が $-50$   →  速さ $50$

＜混乱注意＞原点は左下、$y$ 軸と交わっている点が切片となります。

【例題①】$\textcolor{green}{4200\rm m}$ 離れた家と図書館の間を、姉は家から図書館へ、妹は図書館から家へ向かいました。$\textcolor{green}{x}$ 分後の家までの距離を $\textcolor{green}{y}$ として、次の問いに答えなさい。

(1) 姉と妹それぞれの式を求めなさい。

姉：原点を通るので比例。$\textcolor{blue}{y=ax}$に（$30,4200$）を代入。これ解いて、$\textcolor{red}{y=140x}$

妹：切片が $4200$ の一次関数。$\textcolor{blue}{y=ax+b}$ に（$40,0$）を代入。これを解いて、$\textcolor{red}{y=-105x+4200}$

(2) $\textcolor{green}{2}$ 人が出会うのはおよそ何分後か求めなさい。

$2$ 人が出会うのは $\textcolor{blue}{2}$ 直線の交点（連立方程式の代入法）

$140x=-105x+4200$　

これを解いて、$\textcolor{blue}{x=17.14…}$

およそ $\textcolor{red}{17}$ 分後

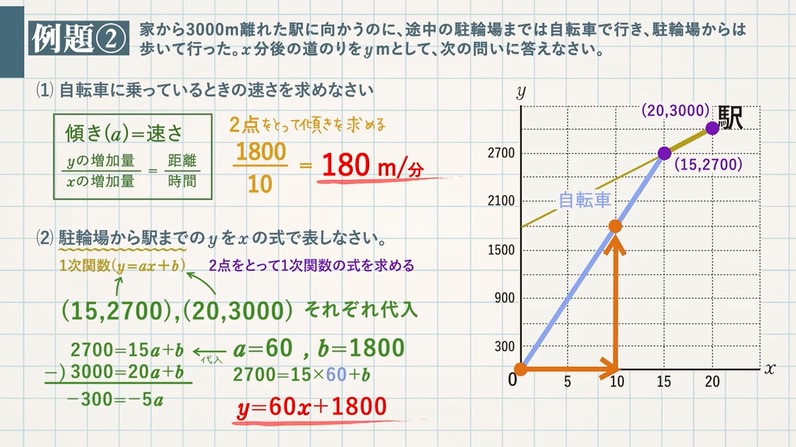
【例題②】家から $\textcolor{green}{3000\rm m}$ 離れた駅に向かうのに、途中の駐輪場までは自転車で行き、駐輪場からは歩いて行った。$\textcolor{green}{x}$ 分後の道のりを $\textcolor{green}{y\rm m}$ として、次の問いに答えなさい 

(1) 自転車に乗っているとの速さを求めなさい。

傾き（$\textcolor{blue}{a}$）$\textcolor{blue}{=}$ 速さ　$10$ 分間で $1800\rm m$ 進むので、

\begin{eqnarray} \frac{yの増加量}{xの増加量}=\frac{距離}{時間}=\frac{1800}{10} =\textcolor{red}{180\rm m/分}\end{eqnarray}

(2) 駐輪場から駅までの $\textcolor{green}{y}$ を $\textcolor{green}{x}$ の式で表しなさい。

$2$ 点(紫)をとって $1$ 次関数の式（$y=ax+b$）を求める。

$2$ 点（$15,2700$）,（$20,3000$）をそれぞれ代入

\begin{eqnarray} \begin{cases} 2700 = 15a+b & \\ 3000 = 20a+b & \end{cases}　 これを解くと、\textcolor{blue}{a=60,b=1800} \end{eqnarray}

よって、$\textcolor{red}{y=60x+1800}$