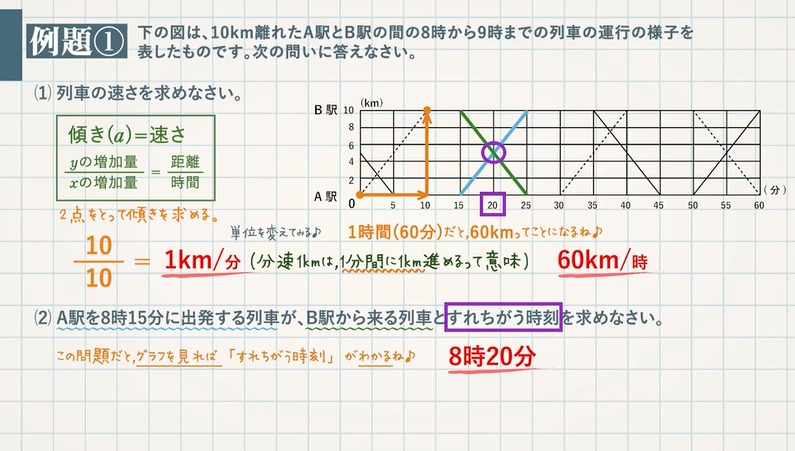
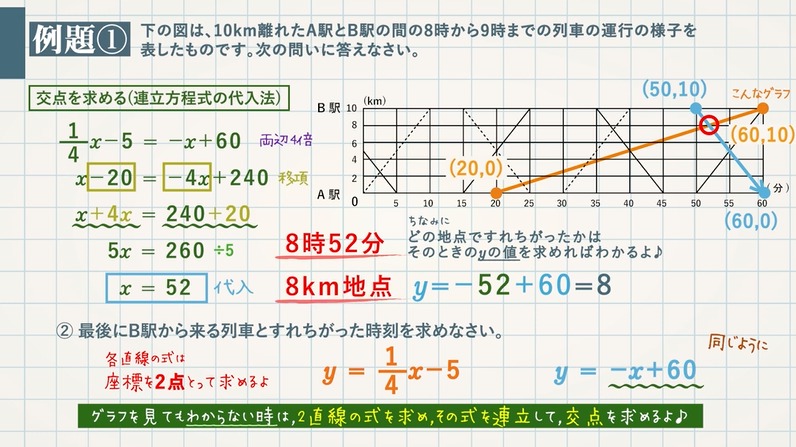
【例題①】図は、$\textcolor{green}{10\rm km}$ 離れたA駅とB駅の間の $\textcolor{green}{8}$ 時から $\textcolor{green}{9}$ 時までの列車の運行の様子を表したものです。次の問いに答えなさい。

(1) 列車の速さを求めなさい。

\begin{eqnarray} & &\textcolor{blue}{傾き（a）}&\textcolor{blue}{=}&\textcolor{blue}{速さ}\\ & &\textcolor{blue}{\frac{y の増加量}{x の増加量}}&\textcolor{blue}{=}&\textcolor{blue}{\frac{距離}{時間}} \end{eqnarray}

$10$ 分で $10$ km 進むので、その速さは $\frac{10}{10}=\textcolor{Red}{1}$ km/分　

分速 $1$ km を 時速に変えると、$1$ 時間($60$ 分)なので、$\textcolor{red}{60}$ km/時 

(2) A駅を $\textcolor{green}{8}$ 時 $\textcolor{green}{15}$ 分に出発する列車が、B駅から来る列車とすれちがう時刻を求めなさい。

「すれちがう時刻」→　$\textcolor{blue}{2}$ 直線の交点を求める。(この問題の場合はグラフを見ればわかります。)　$\textcolor{red}{8}$ 時 $\textcolor{red}{20}$ 分

(3) 太郎さんは、自転車で $\textcolor{green}{8}$ 時 $\textcolor{green}{20}$ 分にA駅を出発して、線路沿いの道をB駅まで時速 $\textcolor{green}{15}$ km で走っていました。次の問いに答えなさい。

① B駅につくまでにB駅から来る列車と何回すれちがうか求めなさい。

太郎さん→時速($60$ 分で) $15$ km なので $\textcolor{blue}{40}$ 分間で、

$15$ km $×$ $\frac{40}{60}=\textcolor{blue}{10}$ km 進むことができます。(図のオレンジの直線)

B駅から来る列車→図の水色の直線

「すれちがう」→ $\textcolor{blue}{2}$ 直線の交点となるので、すれちがった回数は $\textcolor{red}{3}$ 回(図の赤い〇)となります。

②最後にB駅から来る列車とすれちがった時刻を求めなさい。

グラフを見てもわからないときは、$\textcolor{blue}{2}$ 直線の式を求め、その式を連立して交点を求めます。各直線(オレンジと水色)の式は座標を $2$ 点とって求めます。

太郎さん(オレンジ)：（$20$,$0$）,（$60$,$10$）

\begin{eqnarray} \begin{cases} 0= 20a+b & \\ 10 = 60a+b & \end{cases}　これを解いて、\textcolor{blue}{a=\frac{1}{4},b=-5} \end{eqnarray}

よって、その式は $\textcolor{blue}{y=\frac{1}{4}x-5}$・・・①

Ｂ駅からの最後の列車(水色)：（$50$,$10$）,（$60$,$0$）

\begin{eqnarray} \begin{cases} 10= 50a+b & \\ 0 = 60a+b & \end{cases}　これを解いて、\textcolor{blue}{a=-1,b=60} \end{eqnarray}

よって、その式は $\textcolor{blue}{y=-x+60}$・・・②

①,②の式を代入法で解くと、$\textcolor{blue}{x=52}$

よって、$\textcolor{red}{8}$ 時 $\textcolor{Red}{52}$ 分

ちなみに、どの地点ですれちがったかは、そのときの $y$ の値を求めればわかります。$y=-52+60=\textcolor{blue}{8}$　   $\textcolor{red}{8}$ km地点