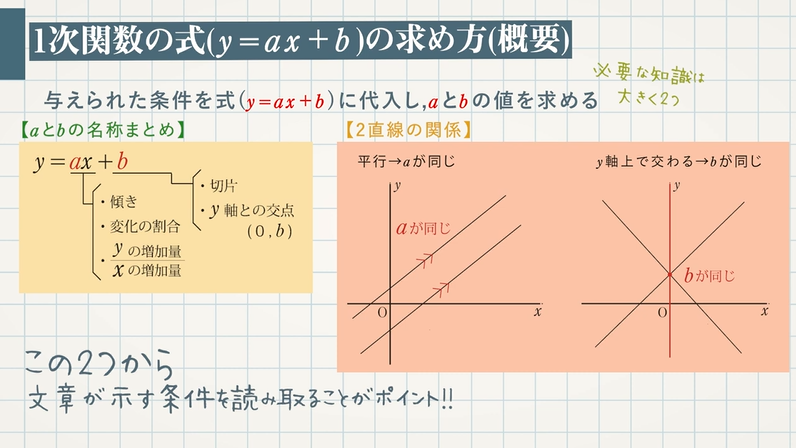
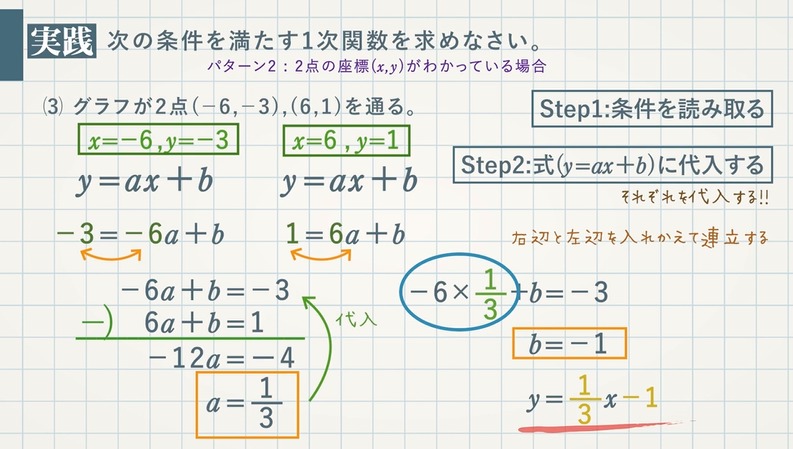
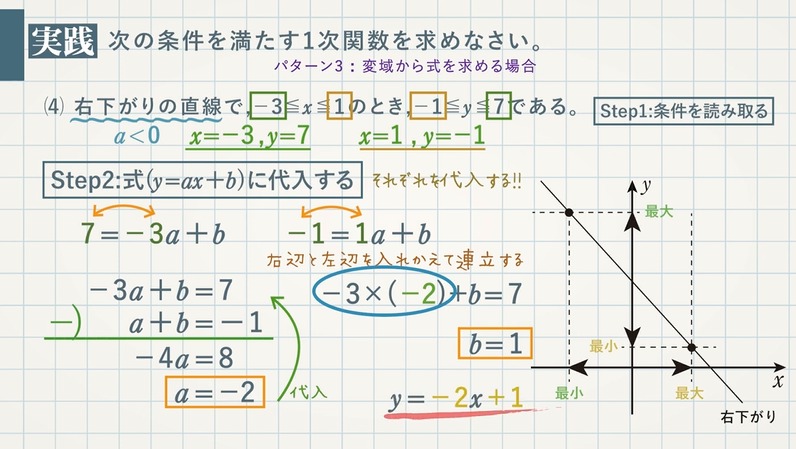
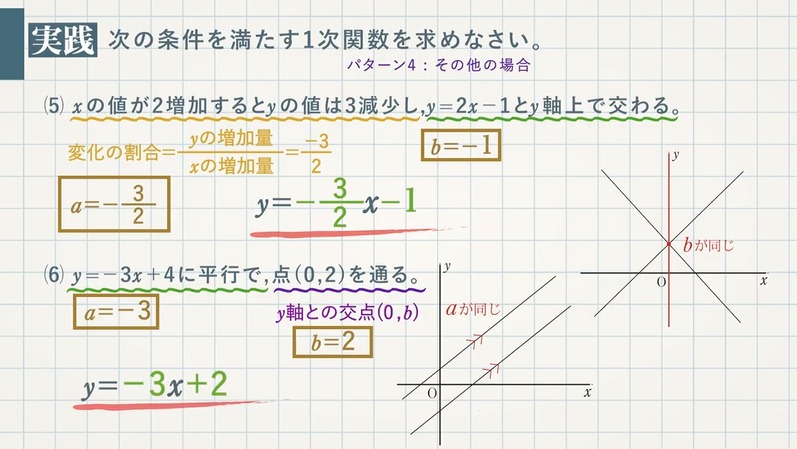
１次関数（直線）の式は、傾き $\textcolor{blue}{a}$ と切片$\textcolor{blue}{b}$ がわかれば、求めることができます。１次関数の式 $\textcolor{blue}{y=ax+b}$ に与えられた条件を代入し、$\textcolor{blue}{a,b}$ の値を求めましょう。

必要な知識を確認

\begin{eqnarray} \textcolor{blue}{a}&=&\textcolor{blue}{傾き}=\textcolor{blue}{変化の割合}=\textcolor{blue}{\frac{y の増加量}{x の増加量}}\\ \textcolor{blue}{b}&=&\textcolor{blue}{切片}=\textcolor{blue}{y 軸との交点} \end{eqnarray}

２直線が平行　→　$\textcolor{blue}{a}$ が同じ

２直線が $\textcolor{blue}{y}$ 軸上で交わる　→　$\textcolor{blue}{b}$ が同じ

【実践】次の条件を満たす $\textcolor{green}{1}$ 次関数を求めなさい。

(1) 変化の割合が $\textcolor{green}{-4}$ で、$\textcolor{green}{x=-1}$ のとき、$\textcolor{green}{y=6}$ となる。

Step１：条件を読み取る

$a=-4$ , $x=-1$ , $y=6$ 

Step２：式（$\textcolor{blue}{y=ax+b}$）に代入する

$6=-4×-1+b$　　　$\textcolor{blue}{b=2}$

よって、$\textcolor{red}{y=-4x+2}$

(2) 切片が $\textcolor{green}{-3}$ で、点 $\textcolor{green}{( 2 , 3 )}$を通る。

Step１：条件を読み取る

$b=-3$ , $x=2$ , $y=3$ 

Step２：式（$\textcolor{blue}{y=ax+b}$）に代入する

$3=2a-3$　　　$\textcolor{blue}{a=3}$

よって、$\textcolor{red}{y=3x-3}$

(3) グラフが２点 $\textcolor{green}{(-6,-3) , (6,1)}$ を通る。

Step１：条件を読み取る

$x=-6$ , $y=-3$　　$x=6$ , $y=1$

Step２：式（$\textcolor{blue}{y=ax+b}$）に代入する（２つの式を連立する）

$-3=-6a+b　,　1=6a+b$

\begin{eqnarray}\begin{cases} -6a + b = -3 & \\ 6a + b = 1 & \end{cases}　これを解くと、\textcolor{blue}{a=\frac{1}{3} , b=-1} \end{eqnarray}

よって、$\textcolor{red}{y=\frac{1}{3}x-1} $

(4) 右下がりの直線で、$\textcolor{green}{-3≦x≦1}$ のとき、$\textcolor{green}{-1≦y≦7}$ である。

Step１：条件を読み取る

右下がりの直線なので、$x=-3$ , $y=7$　　$x=1$ , $y=-1$

Step２：式（$\textcolor{blue}{y=ax+b}$）に代入する（２つの式を連立する）

$7=-3a+b　,　-1=a+b$

\begin{eqnarray}\begin{cases} -3a + b = 7 & \\ a + b = -1 & \end{cases}　これを解くと、\textcolor{blue}{a=-2 , b=1} \end{eqnarray}

よって、$\textcolor{red}{y=-2x+1}$

(5) $\textcolor{green}{x}$ の値が $\textcolor{green}{2}$ 増加すると $\textcolor{green}{y}$ の値は $\textcolor{green}{3}$ 減少し、$\textcolor{green}{y=2x-1}$ と $y$ 上で交わる。

Step１：条件を読み取る

$x$ が $2$ 増加すると $y$ は $3$ 減少 → $\textcolor{blue}{a=-\frac{3}{2}}$

$y=2x-1$ と $y$ 軸上で交わる → $\textcolor{blue}{b=-1}$

よって、$\textcolor{red}{y=-\frac{3}{2}x-1} $

(6) $\textcolor{green}{y=-3x+4}$ に平行で、点 $\textcolor{green}{( 0 , 2 )}$ を通る。

Step１：条件を読み取る

$y=-3x+4$ に平行 → $\textcolor{blue}{a=-3}$

点 $( 0 , 2 )$ を通る。→ $\textcolor{blue}{b=2}$

よって、$\textcolor{red}{y=-3x+2}$