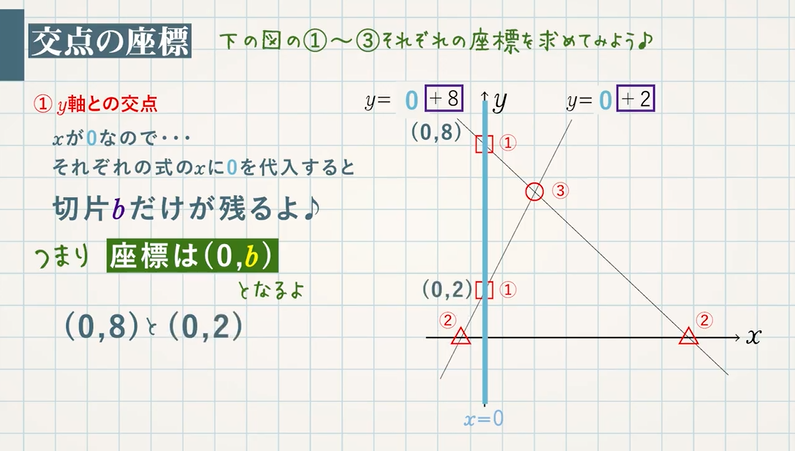
２つのグラフ　$y=-x+8$ , $y=2x+2$ について, まずは ① $\textcolor{green}{y}$ 軸との交点の座標 を求めましょう。

$y$ 軸との交点は $\textcolor{blue}{x}$ が $\textcolor{blue}{0}$ なので・・・それぞれの式の $x$ に $0$ を代入すると切片$\textcolor{blue}{b}$ だけが残ります。つまり、座標は$(0,\textcolor{blue}{b})$ となります。

$y=\textcolor{blue}{0}+8$　　　$y=\textcolor{blue}{8}$

$y=\textcolor{blue}{0}+2$　　　$y=\textcolor{blue}{2}$

よって、その座標は　$\textcolor{red}{(0,8)}$ , $\textcolor{red}{(0,2)}$

続いては ② $\textcolor{green}{x}$ 軸との交点の座標 を求めましょう。

$x$ 軸との交点は $\textcolor{blue}{y}$ が $\textcolor{blue}{0}$ なので・・・それぞれの式の $y$ に $0$ を代入すると

$0=-x+8$　　$x=\textcolor{blue}{8}$

$0=2x+2$　 　$x=\textcolor{blue}{-1}$

よって、その座標は　$\textcolor{red}{(8,0)}$ , $\textcolor{red}{(-1,0)}$

続いては最重要問題です。③２直線の交点の座標 を求めましょう。

これは、連立方程式の解が交点の座標になります。２つの直線の式の連立方程式を解いて $x$ , $y$ の値を求めましょう。

\begin{eqnarray} \begin{cases} y = -x+8 & \\ y = 2x+2 & \end{cases} 　\textcolor{blue}{代入法で解く}　\end{eqnarray}

\begin{eqnarray} 2x+2&=&-x+8\\ 3x&=&6\\ x&=&\textcolor{blue}{2}\\\\ y&=&-2+8\\ y&=&\textcolor{blue}{6} \end{eqnarray}

よって、交点の座標は $\textcolor{red}{(2,6)}$

$\textcolor{green}{x}$ 軸を底辺とする三角形(水色)の面積を求めましょう。

底辺は $x$ 座標なので、$-1→8＝9$

高さは $y$ 座標なので、$6$

よって、面積は $9×6×\frac{1}{2}=\textcolor{red}{27}$

$\textcolor{green}{y}$ 軸を底辺とする三角形(ピンク)の面積を求めましょう。

底辺は $y$ 座標なので、$2→8＝6$

高さは $x$ 座標なので、$2$

よって、面積は $6×2×\frac{1}{2}=\textcolor{red}{6}$ 

グラフ上の四角形の面積を求めましょう。

ポイント：複数の三角形の面積を足す・引く

上の四角形(緑色)の面積を求めましょう。

四角形(緑色)は、三角形(水色) $+$ 三角形(ピンク)なので、

　$27+6＝\textcolor{red}{33}$

四角形(黄色)の面積を求めましょう。

四角形(黄色)は、三角形(緑色)－三角形(ピンク)であり、

三角形(緑色)の面積$=8×8×\frac{1}{2}=32$ なので、

　$32-6＝\textcolor{red}{26}$