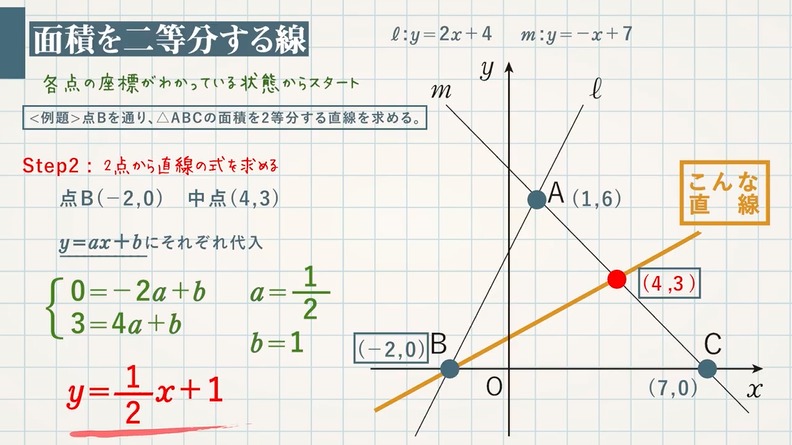
＜例題＞点Bを通り、△ABCの面積を２等分する直線の式を求めなさい。

（必要な座標がわかっている状態からスタート）

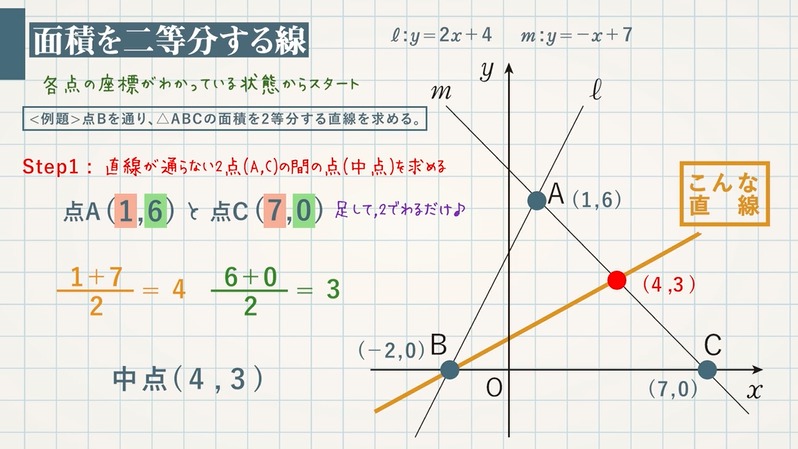
Step１：直線が通らない２点（A,C）の中点を求める。

点A（$1,6$）、点C（$7,0$）　中点は、足して $\textcolor{blue}{2}$ でわるだけ

\begin{eqnarray} \frac{1+7}{2}=\textcolor{blue}{4}　　\frac{6+0}{2}=\textcolor{blue}{3}\\\\ \end{eqnarray}

よって、中点の座標は $\textcolor{blue}{（4,3）}$

Step２：２点から直線の式を求める

$2$ 点の座標より、直線の式を求めます。

点B（$-2,0$）　中点（$4,3$）

$y=ax+b$ にそれぞれを代入して連立

\begin{eqnarray} \begin{cases} 0 = -2a+b & \\ 3 = 4a+b & \end{cases}　 これを解いて、\textcolor{blue}{a=\frac{1}{2},b=1} \end{eqnarray}

よって、点Bを通り、△ABCの面積を２等分する直線の式は $\textcolor{red}{y=\frac{1}{2}x+1}$ となります。

＜例題＞△ABCと面積が等しい△ACPの $\textcolor{green}{y}$ 軸上の点Pの座標を求めなさい。

等積変形：底辺と高さが等しい三角形は面積が等しい。

底辺に平行で頂点を通る直線をひく。底辺が同じとき、この直線上に頂点がある三角形の面積は等しくなる。

△ABCの底辺AC（直線 $\textcolor{blue}{m}$）に平行で、頂点B（$-3,0$）を通る直線の式（図オレンジの直線）を求めます。

平行な直線は傾き($a$)が等しいので、$\textcolor{blue}{a=3}$

点B（$-3,0$）を通るので、　$\textcolor{blue}{x=-3 , y=0}$

$y=ax+b$ に代入すると、

$0=3×(-3)+b　　\textcolor{blue}{b=9}$

点Pは $y$ 軸上の点(切片)なので、点P（$\textcolor{red}{0,9}$）