変域とは $x$ や $y$  (変数) がとることのできる値の範囲をいい、不等号を使って表します。

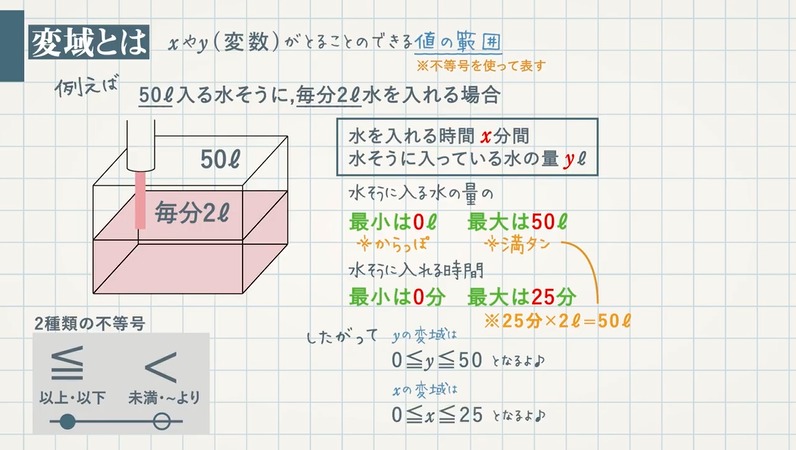
$\textcolor{green}{50}$ℓ 入る水そうに、毎分 $\textcolor{green}{2}$ℓ 水を入れる場合,$\textcolor{green}{x}$ 分間水を入れたときの水そうに入っている水の量を $\textcolor{green}{y}$ℓ とすると、

水そうに入る水の量の最小は $\textcolor{blue}{0ℓ}$ (からっぽ)、最大は $\textcolor{blue}{50ℓ}$ (満タン) となります。よって、$y$ の変域は、$\textcolor{red}{0≦y≦50}$ となります。

水そうに入れる時間の最小は $\textcolor{blue}{0}$ 分、最大は 毎分 $2ℓ×25$ 分 $＝\textcolor{blue}{50ℓ}$ より、$\textcolor{blue}{25}$ 分となります。よって、$x$ の変域は、$\textcolor{red}{0≦x≦25}$ となります。

変域が指定されたグラフのかき方をみていきましょう。

【例題 $\textcolor{green}{1}$ 】 次の $\textcolor{green}{1}$ 次関数のグラフをかきなさい。

　$\textcolor{green}{y=\frac{3}{4}x-2　(-4<x≦4)}$

　$y$ 軸との交点（切片）$=-2$

\begin{eqnarray}\textcolor{blue}{a  = 変化の割合 =}\textcolor{blue}{\frac{y の増加量}{x の増加量}} なので、\\x が 4 増加すると、y が 3 増加する。\end{eqnarray}

Step１　式のグラフをかく

①　切片に点をとる

②　$a$ を分数になおし、点をとる

③　２点を通る直線をひく

Step２　変域をとる

①　変域外のグラフの線を消す

②　両端に点をかく　（＜は○、≦は●で表します。）

【例題 $\textcolor{green}{2}$ 】次の $\textcolor{green}{1}$ 次関数について、$\textcolor{green}{x}$ の変域が $\textcolor{green}{-1<x≦2}$ のときの $\textcolor{green}{y}$ の変域を求めなさい。

Step１　$\textcolor{blue}{x}$ の値を式に代入する

Step２　$\textcolor{blue}{y}$ の値を小さい順に並べる

※並べるときの不等号 (≦なのか＜なのか) は合わせましょう。

①　$\textcolor{green}{y=3x+1}$

　　$x=-1$ のとき、$y=-2$

　　$x=2$ のとき、$y=7$　　よって、$\textcolor{red}{-2<y≦7}$

②　$\textcolor{green}{y=-x+2}$

　　$x=-1$ のとき、$y=3$

　　$x=2$ のとき、$y=0$　　よって、$\textcolor{red}{0≦y<3}$

【例題 $\textcolor{green}{3}$ 】 $\textcolor{green}{1}$ 関数 $\textcolor{green}{y=ax+3}$ で、$\textcolor{green}{x}$ の変域が $\textcolor{green}{-6≦x≦3}$ のときの $\textcolor{green}{y}$ の変域は $\textcolor{green}{1≦y≦b}$ である。$\textcolor{green}{a<0}$ のとき、$\textcolor{green}{a,b}$ の値を求めなさい。

右下がり($a<0$) の $1$ 次関数では、$x$ の値が増加(減少)するほど $y$ の値は減少(増加)するので、

　$x$ が $3$ (最大)  のとき→ $y$ の値が最小

　$x$ が $-6$ (最小) のとき→ $y$ の値が最大

Step $\textcolor{blue}{1}$　式に $\textcolor{blue}{x,y}$ の値を代入し、$\textcolor{blue}{a}$ を求める

\begin{eqnarray}1&=&3a+3　　\textcolor{red}{a=-\frac{2}{3}} \end{eqnarray}

Step $\textcolor{blue}{2}$　$\textcolor{blue}{a}$ の値を入れた式にもう一方の $\textcolor{blue}{x}$ の値を代入する

\begin{eqnarray} y=\frac{2}{3}×(-6)+3=7　　\textcolor{red}{b=7}\end{eqnarray}