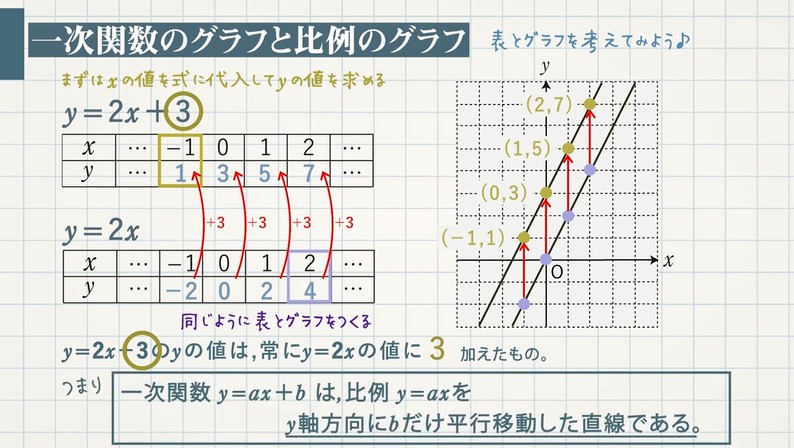
$y=2x+3$ と $y=2x$ のグラフを比べて、どんなことがいえるか確認しましょう。

　$y=2x+3$

　$y=2x$

$y=2x+3$ の $y$ の値は、常に $y=2x$ の値に $3$ を加えたものだとわかります。

つまり、一次関数 $y=ax+b$ のグラフは比例の関係 $y=ax$ のグラフを $\textcolor{blue}{y}$ 軸方向に $\textcolor{blue}{b}$ だけ平行移動した直線になります。

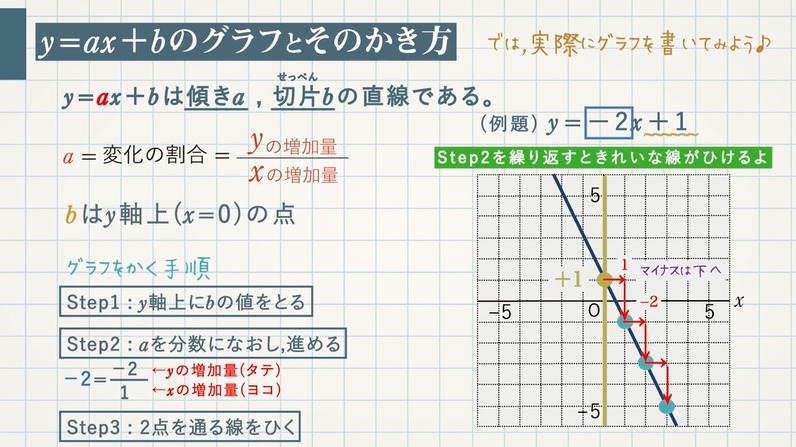
$y=ax+b$ は傾き $\textcolor{blue}{a}$ 、切片 $\textcolor{blue}{b}$ の直線となります。

\begin{eqnarray} a=変化の割合=\frac{\textcolor{blue}{y の増加量}}{\textcolor{blue}{x の増加量}}　b は y 軸上(x=0)の点\end{eqnarray} 　　

グラフをかく手順を $\textcolor{green}{y=-2x+1}$ で確認しましょう。

Step $\textcolor{blue}{1}$：$\textcolor{blue}{y}$ 軸上に $\textcolor{blue}{b}$ の値をとる。今回は $b=1$

Step $\textcolor{blue}{2}$：$\textcolor{blue}{a}$ を分数になおし、進める。

\begin{eqnarray} a=-2=\frac{-2　←\textcolor{blue}{y の増加量(タテ)}}{1　←\textcolor{blue}{x の増加量(ヨコ)}} \end{eqnarray} 　

Step $\textcolor{blue}{3}$：$\textcolor{blue}{2}$ 点を通る線をひく。

($0,1$) , ($1,-1$) を通る直線をひく。

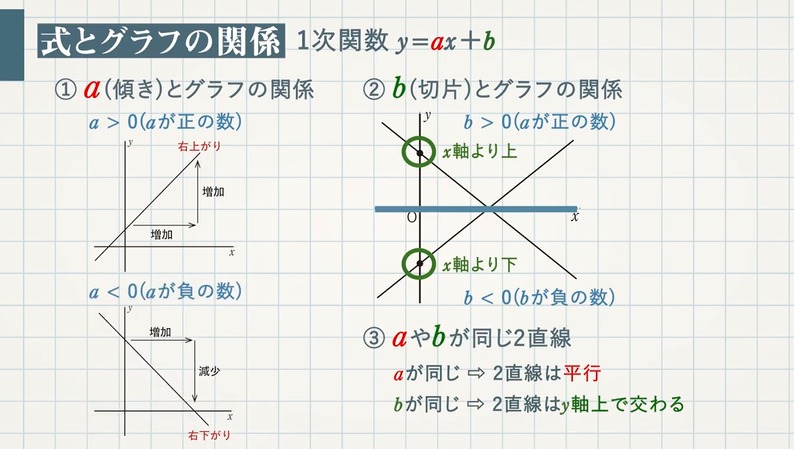
$a＞0$　 ($a$ が正の数)のときは、右上がりのグラフになります。$x$ が増加すれば、$y$ も増加し、$x$ が減少すれば、$y$ も減少するので、変化の割合($a$)は正の数となります。

$a＜0$　 ($a$ が負の数)のときは、右下がりのグラフになります。$x$ が増加すれば、$y$ は減少し、$x$ が減少すれば、$y$ は増加するので、変化の割合($a$)は負の数となります。

傾き($\textcolor{blue}{a}$)が同じ $\textcolor{blue}{2}$ 直線→ $\textcolor{blue}{2}$ 直線は平行

切片($\textcolor{blue}{b}$)が同じ $\textcolor{blue}{2}$ 直線→ $\textcolor{blue}{2}$ 直線は $\textcolor{blue}{y}$ 軸上で交わる