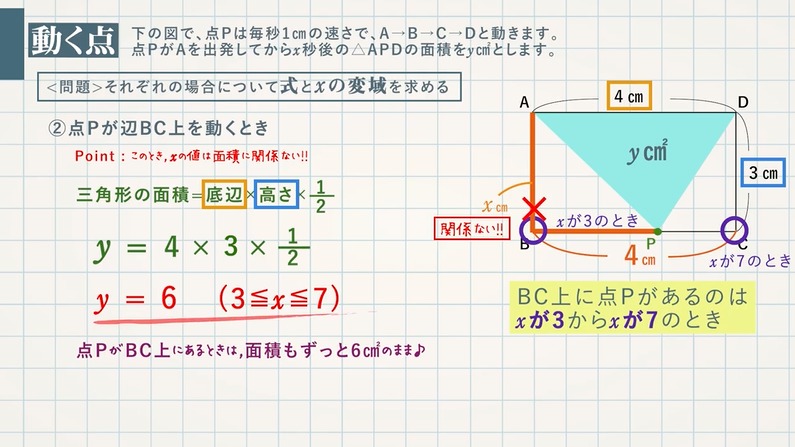
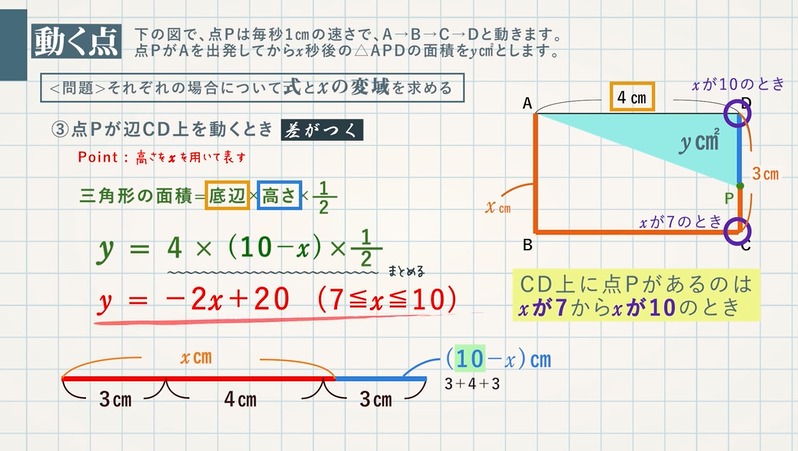
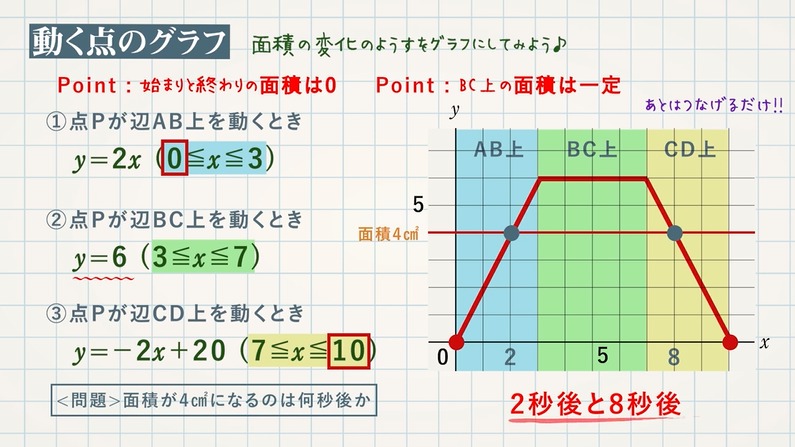
【問題】図で、点Pは毎秒 $\textcolor{green}{1\rm cm}$ の速さで、A→B→C→Dと動きます。点PがAを出発してから $\textcolor{green}{x}$ 秒後の△APDの面積を $\textcolor{green}{y\rm cm^2}$ とします。

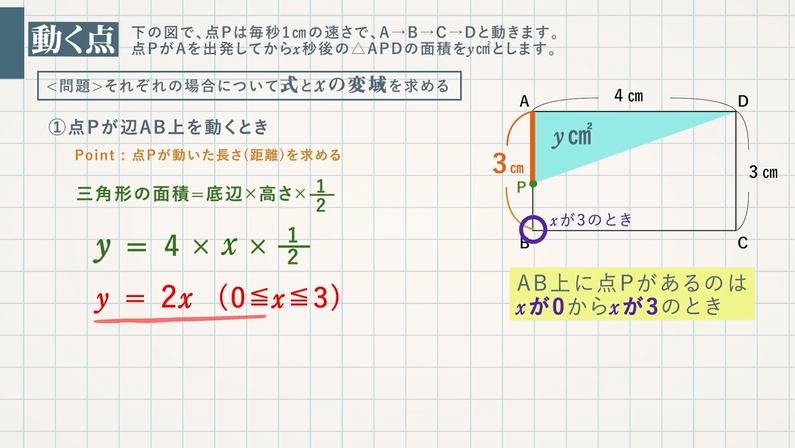
① 点Pが辺AB上を動くときの式と $\textcolor{green}{x}$ の変域を求めなさい。

Point：点Pが動いた長さ（距離）を求める

毎秒 $1\rm cm$ の速さで $x$ 秒動くので、その距離は $1×x=\textcolor{blue}{x}$

三角形の面積 $=$ 底辺 $×$ 高さ $×$ $\frac{1}{2}$ 

$y=4×x×\frac{1}{2}$　　$\textcolor{red}{y=2x}$

辺AB上に点Pがあるのは、$\textcolor{blue}{x}$ が $\textcolor{blue}{0}$ から $\textcolor{blue}{x}$ が $\textcolor{blue}{3}$ のとき

よって、$x$ の変域は $\textcolor{red}{0≦x≦3}$

② 点Pが辺BC上を動くときの式と $\textcolor{green}{x}$ の変域を求める

Point：このとき、$\textcolor{blue}{x}$ の値は面積に関係ない

辺BC上を動くとき、△APDの底辺は $4$ 、高さは $3$ で一定（計算に $\textcolor{blue}{x}$ の値は必要なし）

三角形の面積 $=$ 底辺 $×$ 高さ $×$ $\frac{1}{2}$ 

$y=4×3×\frac{1}{2}$　　$\textcolor{red}{y=6}$

点PがBC上にあるときは、面積はずっと $\textcolor{blue}{6\rm cm^2}$ で一定

辺BC上に点Pがあるのは、$\textcolor{blue}{x}$ が $\textcolor{blue}{3}$ から $\textcolor{blue}{x}$ が $\textcolor{blue}{7}$ のとき

よって、$x$ の変域は $\textcolor{red}{3≦x≦7}$

③ 点Pが辺CD上を動くときの式と $\textcolor{green}{x}$ の変域を求める

Point：高さを $\textcolor{blue}{x} $ を用いて表す

辺CD上を動くとき、高さはA～Dまでの合計（AB+BC+CD）と $\textcolor{blue}{x}$ 秒間に進んだ距離の差になります。

高さ $=(3+4+3)\textcolor{blue}{-}x=\textcolor{blue}{(10-x)\rm cm}$

三角形の面積 $=$ 底辺 $×$ 高さ $×$ $\frac{1}{2}$ 

$y=4×(10-x)×\frac{1}{2}$　　$\textcolor{red}{y=-2x+20}$

辺CD上に点Pがあるのは、$\textcolor{blue}{x}$ が $\textcolor{blue}{7}$ から $\textcolor{blue}{x}$ が $\textcolor{blue}{10}$ のとき

よって、$x$ の変域は $\textcolor{red}{7≦x≦10}$

面積の変化のようすをグラフに表してみましょう。

① 点Pが辺AB上を動くとき　$y=2x$  $(\textcolor{blue}{0}≦x≦3)$

② 点Pが辺BC上を動くとき　$y=6$  $(3≦x≦7)$

③ 点Pが辺CD上を動くとき　$y=-2x+20$  $(7≦x≦\textcolor{blue}{10})$

Point：始まりと終わりの面積は $\textcolor{blue}{0}$

$x=0,10$ のとき、$y=0$ の点をとる（図の赤い点）

Point：辺BC上の面積は一定

$3≦x≦7$ のとき、$y=6$ の直線をひく

あとは点と線をつなげるだけで完成。

問. 面積が $4\rm cm^2$ になるのは何秒後か

グラフより、$\textcolor{red}{2}$ 秒後と $\textcolor{red}{8}$ 秒後（図の青点）