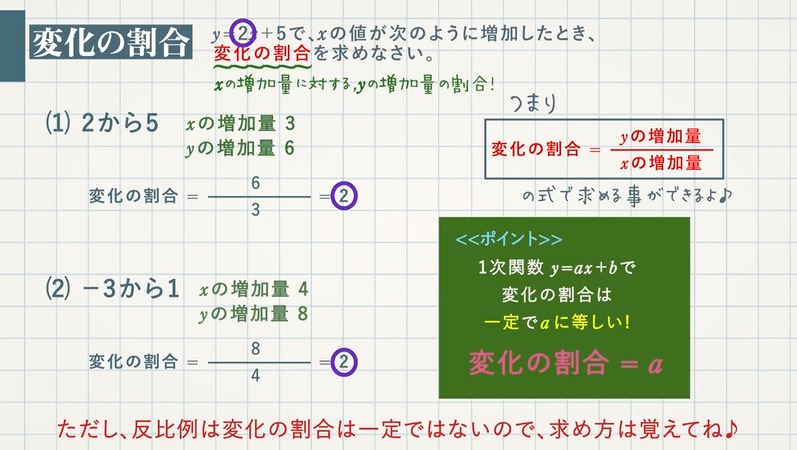
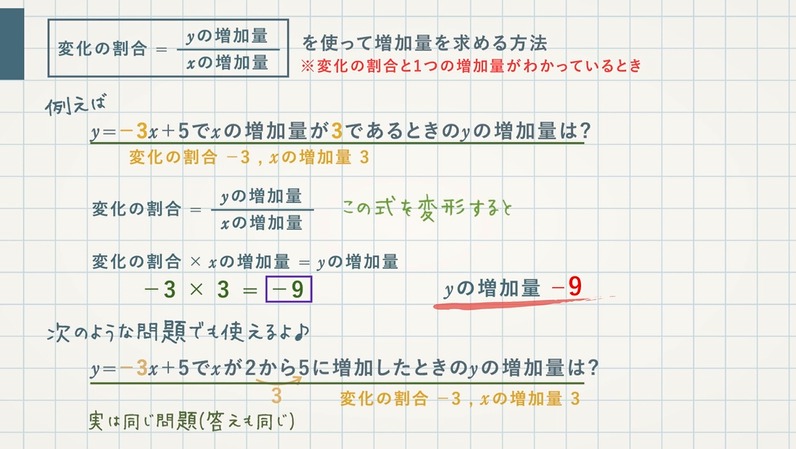
【問題】$\textcolor{green}{y=2x+5}$ で、$\textcolor{green}{x}$の値が次のように増加したとき、$\textcolor{green}{x}$ と $\textcolor{green}{y}$ の増加量を求めなさい。

(1) $\textcolor{green}{2}$ から $\textcolor{green}{5}$　

増加量の求め方：変化後の値 $\textcolor{blue}{-}$ 変化前の値

 $5-2=3$　$\textcolor{red}{x}$ の増加量 $\textcolor{red}{3}$

$y$ の増加量は、$x=2$、$x=5$ のときの $y$ の値を考えます。

$x=2$ のとき　$y=2×2+5=\textcolor{blue}{9}$

$x=5$ のとき　$y=2×5+5=\textcolor{blue}{15}$

$15-9=6$　$\textcolor{red}{y}$ の増加量 $\textcolor{red}{6}$

(2) $\textcolor{green}{-3}$ から $\textcolor{green}{1}$　

増加量の求め方：変化後の値 $-$ 変化前の値

$1-(-3)=4$　$\textcolor{red}{x}$ の増加量 $\textcolor{red}{4}$

$y$ の増加量は、$x=2$、$x=5$ のときの $y$ の値を考えます。

$x=-3$　$y=2×(-3)+5=\textcolor{blue}{-1}$

$x=1$　$y=2×1+5=\textcolor{blue}{7}$

$7-(-1)=8$　$\textcolor{red}{y}$ の増加量 $\textcolor{red}{8}$

$x$ の増加量に対する $y$ の増加量の割合を変化の割合といいます。

\begin{eqnarray} 変化の割合は\textcolor{blue}{\frac{y の増加量}{x の増加量}} で求めることができます。 \end{eqnarray}

【問題】$\textcolor{green}{y=2x+5}$ で、次のときの変化の割合を求めなさい。

(1) $\textcolor{green}{2}$ から$\textcolor{green}{5}$　　$x$ の増加量 $\textcolor{blue}{3}$、$y$ の増加量 $\textcolor{blue}{6}$ なので、

\begin{eqnarray} 　変化の割合　=\textcolor{blue}{\frac{6}{3}}=\textcolor{red}{2} \end{eqnarray}

(2) $\textcolor{green}{-3}$ から$\textcolor{green}{1}$　　$x$ の増加量 $\textcolor{blue}{4}$、$y$ の増加量 $\textcolor{blue}{8}$ なので、

\begin{eqnarray} 　変化の割合　=\textcolor{blue}{\frac{8}{4}}=\textcolor{red}{2} \end{eqnarray}

このように、$1$ 次関数 $y=ax+b$ で変化の割合は一定で $\textcolor{blue}{a}$ に等しくなります。変化の割合 $\textcolor{blue}{=}$$\textcolor{blue}{a}$

\begin{eqnarray} 変化の割合=\frac{y の増加量}{x の増加量} 　を使って増加量を求める方法\end{eqnarray}

※変化の割合と$\textcolor{blue}{x,y}$ のどちらか $\textcolor{blue}{1}$ つの増加量がわかっているとき

【問題】$\textcolor{green}{y=-3x+5}$ で $\textcolor{green}{x}$ の増加量が $\textcolor{green}{3}$ であるときの $\textcolor{green}{y}$ の増加量は？ 

\begin{eqnarray} 変化の割合=\frac{y の増加量}{x の増加量}　を変形すると\end{eqnarray}

変化の割合 $\textcolor{blue}{×}$ $\textcolor{blue}{x}$ の増加量 $\textcolor{blue}{= y}$ の増加量

変化の割合($a$)が $\textcolor{blue}{-3}$ , $x$ の増加量が $\textcolor{blue}{3}$ より、

$-3×3=-9$　　$\textcolor{red}{y}$ の増加量 $\textcolor{red}{-9}$