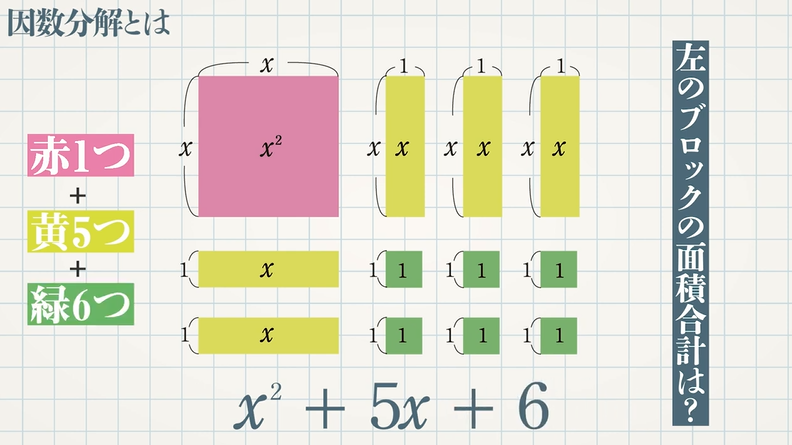多項式を、単項式や多項式の積の形に表す方法を確認しましょう。

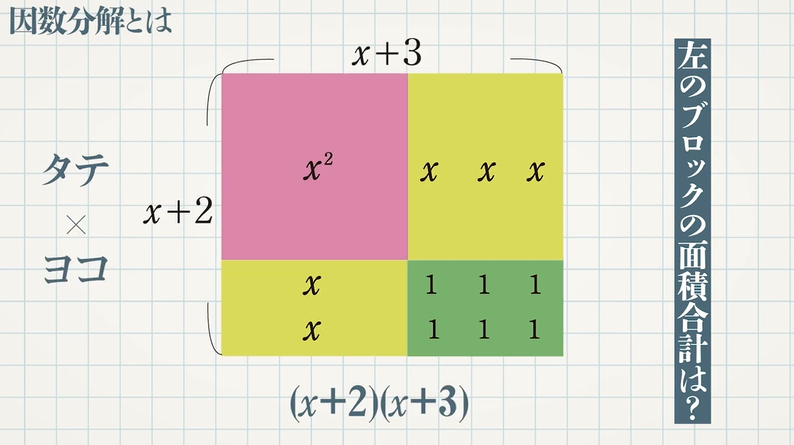
図の各ブロックの面積は

赤：$x×x$ $=\textcolor{blue}{x^2}$　

黄：$x×1×5$ つ $=$ $\textcolor{blue}{5x}$　

緑：$1×1×6$ つ $=$ $\textcolor{blue}{6}$　　

その合計は、赤 $\textcolor{blue}{+}$ 黄 $\textcolor{blue}{+}$ 緑 $\textcolor{blue}{=}$ $\textcolor{blue}{x^2+5x+6}$ と表すことができます。

この図は、先ほどの各ブロックを隙間無く並べたものです。ここで、タテの長さ、ヨコの長さはそれぞれ以下のように表すことができます。

タテの長さ：赤（$x$）$+$   緑（$2$）　→　$\textcolor{blue}{x+2}$

ヨコの長さ：赤（$x$）$+$    緑（$3$）　→　$\textcolor{blue}{x+3}$

ブロックの面積は、タテ $×$ ヨコ $=$ $\textcolor{blue}{(x+2)(x+3)}$と表すこともできます。

これより、$\textcolor{blue}{x^2+5x+6=(x+2)(x+3)}$ となります。

$1$ つの式が多項式や単項式の積の形に表されるとき、積をつくっている $1$ つ $1$ つの式を、もとの式の因数といいます。先ほどの例でいうと、$x+2 , x+3$  が  $x^2+5x+6$  の因数になります。

多項式をいくつかの因数の積に表すことを因数分解するといいます。$x²+5x+6$ を因数分解 → $\textcolor{blue}{(x+2)(x+3)}$ 

※式の展開を逆にみたものが因数分解となります。

  　　  展開：$(x+2)(x+3) →x^2+5x+6$

　因数分解：$　x^2+5x+6 →(x+2)(x+3)$

【問題】次の式を因数分解しなさい。

　　　　$\textcolor{green}{a^2+2ab+b^2}$

問題にある $a^2+2ab+b^2$ は各ブロックの面積の合計です。

タテ $×$ ヨコ $=$ 面積 なので、ブロックのタテの長さ、ヨコの長さが $a^2+2ab+b^2$ の因数となります。

タテの長さ：$a+b$　　ヨコの長さ：$a+b$

因数の積で表すことが因数分解でしたので、

$(a+b)(a+b)=\textcolor{red}{(a+b)^2}$