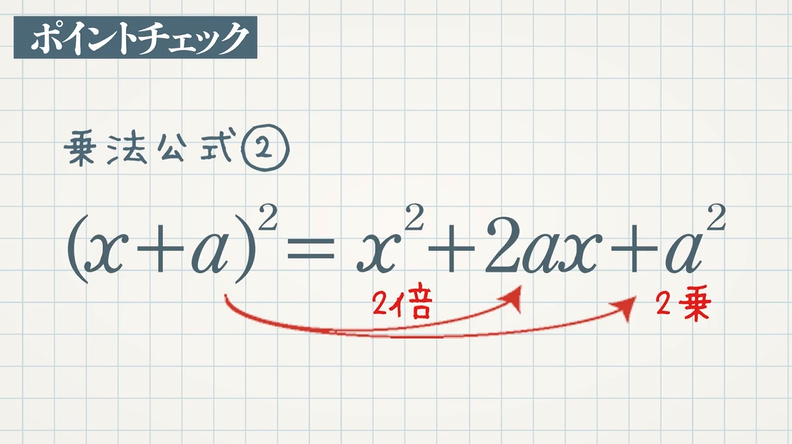因数分解公式②

$\textcolor{blue}{x^2±2ax+a^2=(x±a)^2　a^2±2ab+b^2=(a±b)^2}$

因数分解公式③

$\textcolor{blue}{x^2-a^2=(x+a)(x-a)　a^2－b^2=(a+b)(a-b)}$

因数分解は展開の逆ですので、まずは乗法公式②(③)の復習をしておきましょう。

乗法公式② $\textcolor{blue}{(x+a)^2=x^2+2ax＋a^2}$

$x$ の係数には $a$ の $\textcolor{blue}{2}$ 倍、定数項には  $a$ の $\textcolor{blue}{2}$ 乗が入ります。

乗法公式②を使って $a$ に入る数字を求めましょう。

$x^2+8x+16=(x+a)^2$

まず $\textcolor{blue}{2}$ 乗して $\textcolor{blue}{+16}$ になる数を考えると、$\textcolor{blue}{+4}$ と $\textcolor{blue}{-4}$ の $\textcolor{blue}{2}$ つがあります。このうち、$\textcolor{blue}{2}$ 倍して $\textcolor{blue}{+8}$ になるのは $\textcolor{blue}{+4}$ なので、$\textcolor{blue}{a=+4}$ であることがわかります。よって、$x^2-8x+16$ を因数分解すると $\textcolor{blue}{(x+4)^2}$　

ちなみに、乗法公式③ $\textcolor{blue}{(x-a)^2=x^2-2ax+a^2}$ では、$x^2-8x+16$ は、$\textcolor{blue}{2}$ 倍して$\textcolor{blue}{-8}$ 、$\textcolor{blue}{2}$ 乗して $\textcolor{blue}{+16}$ になる数なので、$x^2-8x+16=\textcolor{blue}{(x-4)^2}$ となります。

続いては因数分解公式③ $\textcolor{blue}{x^2-a^2=(x+a)(x-a)}$です。

こちらも同じく、まずは乗法公式④の確認をしましょう。

乗法公式④ $\textcolor{blue}{(x+a)(x-a)=x^2-a^2}$

【問題】$\textcolor{green}{x^2-49}$ を因数分解しなさい。

因数分解では、展開の逆を考えればいいので、$\textcolor{blue}{2}$ 乗して $\textcolor{blue}{49}$ になる数を求めると、$\textcolor{blue}{a=7}$ であるとわかります。

よって、$x^2-49$ を因数分解すると、$\textcolor{red}{(x+7)(x-7)}$

公式②,③を使ういろいろな因数分解について確認しましょう。

【発展】次の式を因数分解しなさい。

③ $\textcolor{green}{4a^2-12ab+9b^2}$　　 $\textcolor{blue}{a^2±2ab+b^2=(a±b)^2}$

$4a^2=\textcolor{blue}{(2a)^2}$　$9b^2=\textcolor{blue}{(3b)^2}$　$-12ab=\textcolor{blue}{-2×2a×3b}$

より、$\textcolor{red}{(2a-3b)^2}$ となります。

② $\textcolor{green}{64x^2-100y^2}$　$\textcolor{blue}{a^2-b^2=(a+b)(a-b)}$ 

$64x^2=\textcolor{blue}{(8x)^2}$　　$100y^2=\textcolor{blue}{(10y)^2}$ 

より、$\textcolor{red}{(8x+10y)(8x-10y)}$ となります。

【問題】$\textcolor{green}{\rm A,B}$ の内、正しい方を $\textcolor{green}{1}$ つ選びなさい。

① $\textcolor{green}{x^2-9}$　$\textcolor{blue}{x^2-a^2=(x+a)(x-a)}$ なので、

　A. $\textcolor{red}{(x+3)(x-3)}$

② $\textcolor{green}{4x^2+4xy+y^2}$　$\textcolor{blue}{a^2+ab+b^2=(a+b)^2}$ なので、

　B. $\textcolor{red}{(2x+y)^2}$

③ $\textcolor{green}{a^2-\frac{1}{16}}$　$\textcolor{blue}{a^2-b^2=(a+b)(a-b)}$ なので、

　A. $\textcolor{red}{(a+\frac{1}{4})(a-\frac{1}{4})}$