$\sqrt{　}$ やπといった無理数でも、整数部分については、はっきりわかります。

$π＝3.14159$　・・・　整数部分 $3$

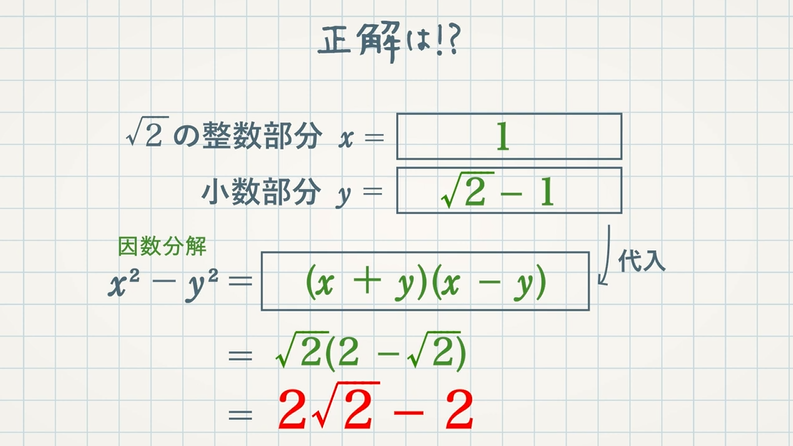
$\sqrt{2}=1.41421$　・・・　整数部分 $1$　

では、小数部分はどうでしょうか？

これは無限に続いているのではっきりわかりません。

そこで次のように表します。

小数部分 → 元の数 $\textcolor{blue}{-}$ 整数の部分

例えば、$\sqrt{2}$ であれば、その小数部分は$\textcolor{blue}{\sqrt{2}-1}$ と表すことができます。

$\sqrt{5}=2.2360679$・・・なので、その整数部分は $2$ 、小数部分は $\textcolor{blue}{\sqrt{5}-2}$ となりますが、例えば $\sqrt{30}$ や $\sqrt{60}$ では近似値がわからないので、整数部分がわかりません。そういうときは、数直線で整数部分を考えましょう。

$\sqrt{30}$ は $5(=\sqrt{25})$ と $6(=\sqrt{36})$ の間にあるので、その整数部分は $\textcolor{blue}{5}$ になります。

$\sqrt{60}$ は $7(=\sqrt{49})$ と $8(=\sqrt{64})$ の間にあるので、その整数部分は $\textcolor{blue}{7}$ になります。

【問題】$\textcolor{green}{\sqrt{2}}$ の整数部分を $\textcolor{green}{x}$ 、小数部分を $\textcolor{green}{y}$ とするとき、$\textcolor{green}{x^2-y^2}$ の値を求めなさい。

$\sqrt{2}$ の整数部分 $x＝\textcolor{blue}{1}$

$\sqrt{2}$ の小数部分 $y＝\textcolor{blue}{\sqrt{2}-1}$　をそれぞれ代入。

代入のポイント：式を簡単にしてから代入

$x^2-y^2$ を因数分解すると、$(x+y)(x-y)$

ここで、$x=1$ , $y=\sqrt{2}-1$ を代入

$(1+\sqrt{2}-1)(1-\sqrt{2}+1)$

$=\sqrt{2}(2-\sqrt{2})=\textcolor{red}{2\sqrt{2}-2}$