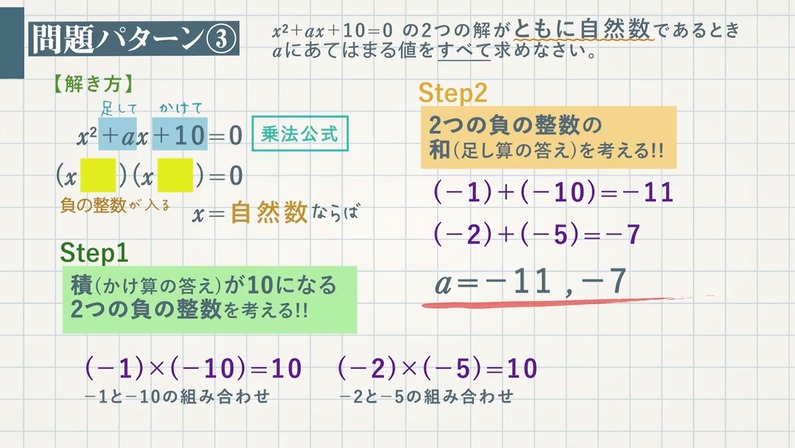
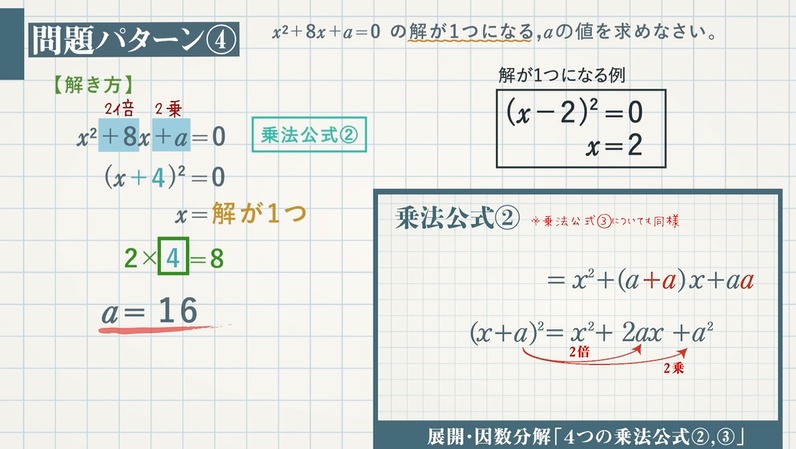
２次方程式を成り立たせる文字の値をその方程式の解といいます。

\begin{eqnarray}  \textcolor{green}{x^2-5x+6}&\textcolor{green}{=}&\textcolor{green}{0}\\ (x-3)(x-2)&=&0\\ \textcolor{red}{x}&\textcolor{red}{=}&\textcolor{red}{3,2}\\\\ \textcolor{green}{(x-2)^2}&\textcolor{green}{=}&\textcolor{green}{0}\\ \textcolor{red}{x}&\textcolor{red}{=}&\textcolor{red}{2} \end{eqnarray}

一般に、２次方程式の解は２つですが、２つの解が一致して１つになることもあります。

【問題パターン①】 $\textcolor{green}{x^2+ax+8=0}$ の解の１つが $\textcolor{green}{2}$ であるとき、$\textcolor{green}{a}$ の値と他の解を求めなさい。

【一般的な解き方】

\begin{eqnarray} 　x^2+ax+8&=&0　　　x=2 を代入\\ \textcolor{red}{a}&\textcolor{red}{=}&\textcolor{red}{-6}\\\\ \end{eqnarray} \begin{eqnarray} x^2\textcolor{blue}{-6}x+8&=&0　　a=-6 を代入\\ (x-4)(x-2)&=&0\\ x&=&\textcolor{red}{4},2 \end{eqnarray}

【その他の解き方】

\begin{eqnarray} x^2+ax\textcolor{blue}{+8}&=&0　 解の 1 つが 2 なので、 \\ (x-2)(x+□)&=&0　 -2×□=\textcolor{blue}{8}\\ (x-2)(x\textcolor{blue}{-4})&=&0　 他の解 \textcolor{red}{x=4}\\a&=&(-4)+(-2)\\\textcolor{red}{a}&\textcolor{red}{=}&\textcolor{red}{-6} \end{eqnarray}

【問題パターン②】 $\textcolor{green}{x^2+ax+b=0}$ の解が $\textcolor{green}{-3,5}$ であるとき、 $\textcolor{green}{a,b}$ の値を求めなさい。

【一般的な解き方】

　$x^2+ax+b$　　$x=-3,5$ をそれぞれ代入

$-3a+b=-9　　  (x=-3)$

　$5a+b=-25　　(x=5)$

連立して解くと、$\textcolor{red}{a=-2,b=-15}$

【その他の解き方】

 $x=-3,5$ より、$(x+3)(x-5)=0$

 $x^2+ax+b=0$　$a$ は「和」$b$ は「積」なので

 $a=3+(-5)=\textcolor{red}{-2}$

 $b=3×(-5)=\textcolor{red}{-15}$

【問題パターン③】 $\textcolor{green}{x^2+ax+10=0}$ の２つの解がともに自然数であるとき $\textcolor{green}{a}$ にあてはまる値をすべて求めなさい。

解がともに自然数ならば、$(x+□)(x+□)=0$　　

□には負の整数が入ります。

Step１：積が $\textcolor{blue}{10}$ になる２つの負の整数を考える

$(\textcolor{blue}{-1})×(\textcolor{blue}{-10})=10$

$(\textcolor{blue}{-2})×(\textcolor{blue}{-5})=10$

Step２：２つの負の数の「和」を考える

$(-1)+(-10)=\textcolor{blue}{-11}$

$(-2)+(-5)=\textcolor{blue}{-7}$

よって、$a$ にあてはまる値は、$\textcolor{red}{-11,-7}$

【問題パターン③】 $\textcolor{green} {x^2+8x+a=0}$ の解が１つになる $\textcolor{green} {a}$ の値を求めなさい。

解が１つになる例

 $(x-2)^2=0$　$x=2$

乗法公式②より、$2$ 倍して $+8$ になる数を考えます。

 $x^2\textcolor{blue}{+8}x+a=0$

 $(x+□)^2=0$

 $2×□=8$　　$□=\textcolor{blue}{4}$

 $(x\textcolor{blue}{+4})^2=0$ より、$a$ には $2$ 乗した数が入ります。

$a=\textcolor{blue}{4^2}=\textcolor{red}{16}$