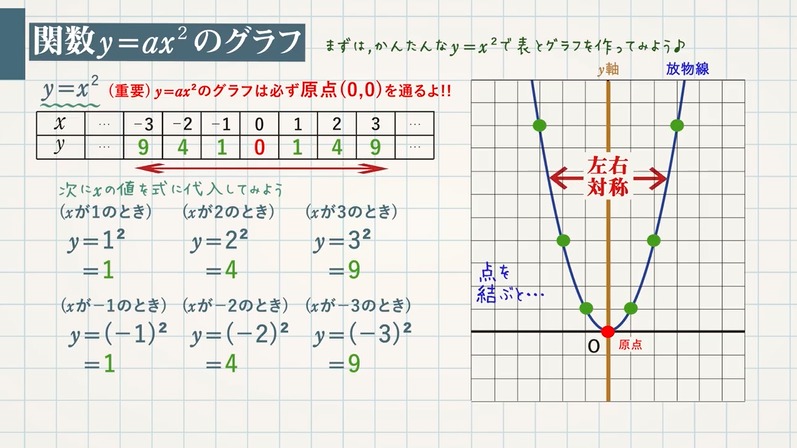
関数 $y=ax^2$ のグラフについて、まずはかんたんな $y=x^2$ で表とグラフを作ってみましょう。

（重要）$\textcolor{blue}{y=ax^2}$ のグラフは必ず原点（$\textcolor{blue}{0,0}$）を通ります。

$x$ の値に対応する $y$ の値を求めましょう。

$x=1$ のとき、$y=\textcolor{blue}{1}$　　　$x=-1$ のとき、$y=\textcolor{blue}{1}$

$x=2$ のとき、$y=\textcolor{blue}{4}$　　　$x=-2$ のとき、$y=\textcolor{blue}{4}$

$x=3$ のとき、$y=\textcolor{blue}{9}$　　　$x=-3$ のとき、$y=\textcolor{blue}{9}$

これらの点を結ぶと、$\textcolor{blue}{y}$ 軸について対称（左右対称）な放物線となっていることがわかります。

関数 $y=ax^2$ のグラフは原点を通り、$\textcolor{blue}{y}$ 軸に対称な放物線となります。

$y=2x^2$ と $y=-2x^2$ のグラフを比べて放物線の向きについて確認しましょう。

$y=2x^2$($a＞0$)は最小値が $\textcolor{blue}{0}$ である上に開く(下に凸)グラフになります。

$y=-2x^2$($a＜0$)は最大値が $\textcolor{blue}{0}$ である下に開く(上に凸)グラフになります。

これらのグラフのように $a$ の絶対値が等しいグラフは、同じ $x$ の値に対応する $y$ の値が、符号が反対のものになります。

$x=1$ のとき、$y=2×1^2=\textcolor{blue}{2}$　   $y=-2×1^2=\textcolor{blue}{-2}$

$x=2$ のとき、$y=2×2^2=\textcolor{blue}{8}$　   $y=-2×2^2=\textcolor{blue}{-8}$

$x=3$ のとき、$y=2×3^2=\textcolor{blue}{18}$　 $y=-2×3^2=\textcolor{blue}{-18}$

$y=ax^2$ で $\textcolor{blue}{a}$ の絶対値が等しいグラフは、$\textcolor{blue}{x}$ 軸について対称となります。

図の黒の放物線を $y=x^2$ とするとき、

$y=\frac{1}{2}x^2$ , $y=2x^2$ がどのような形になるか考えましょう。

$3$ つの式の $x=1$ のときの $y$ の値を求める

$y=\frac{1}{2}x^2=\textcolor{blue}{\frac{1}{2}}$　$\textcolor{blue}{y}$ の値が小 →グラフの開きは大

$y=x^2=\textcolor{blue}{1}$　　 $\textcolor{blue}{y}$ の値が中→グラフの開きは中

$y=x^2=\textcolor{blue}{2}$　　 $\textcolor{blue}{y}$ の値が大→グラフの開きは小

よって、グラフの開きは、$\textcolor{blue}{a}$ の絶対値が大きいほど小さく、$\textcolor{blue}{a}$ の絶対値が小さいほど大きくなります。