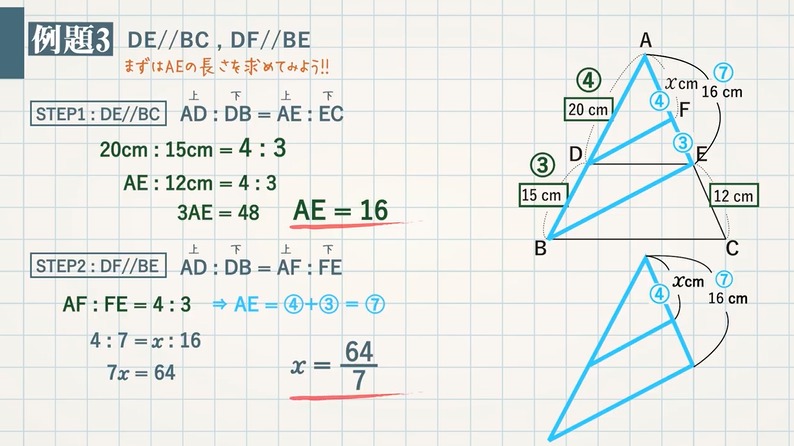
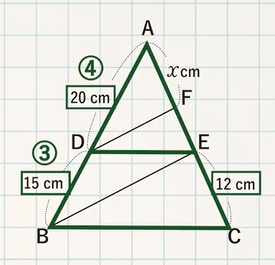
【例題 $\textcolor{green}{1}$ 】 $\textcolor{green}{\rm AB//CD//EF}$
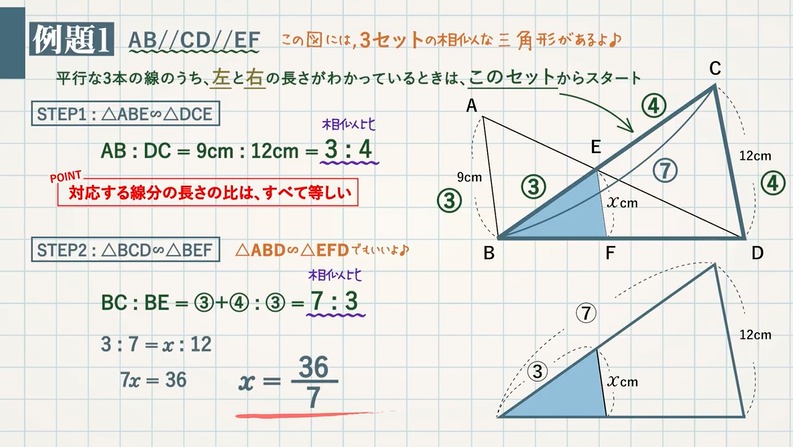
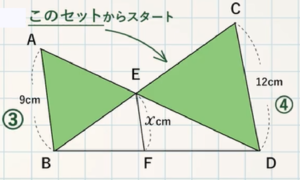
平行な $3$ 本の線のうち、左と右の長さがわかっているときは、$\rm △ABE$ と $\rm △DCE$ からスタート
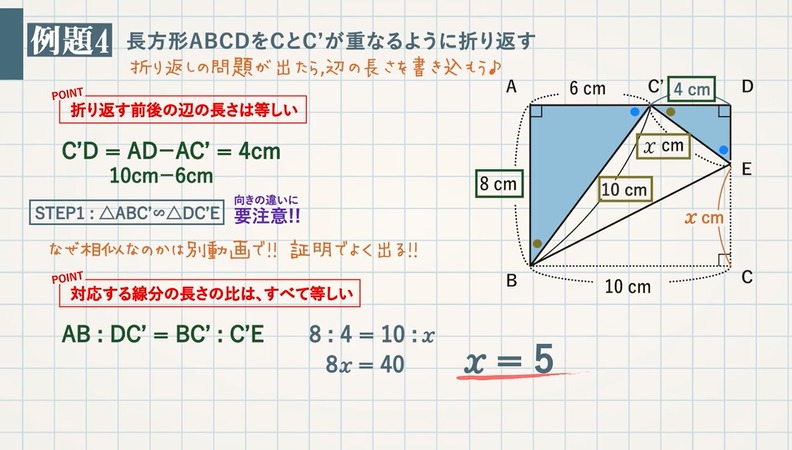
STEP $\textcolor{blue}{1}$:$\textcolor{blue}{\rm △ABE∽△DCE}$
$\rm AB:DC=9cm:12cm=\textcolor{blue}{3:4}$ (相似比)
POINT:対応する線分の長さの比は、すべて等しい
STEP $\textcolor{blue}{2}$:$\textcolor{blue}{\rm △BCD∽△BEF}$($\rm △ABD∽△EFD$ でもOK)
$\textcolor{blue}{\rm BC:BE=③+④:③=7:3}$ (相似比)
$3:7=x:12$ これを解いて、$\textcolor{Red}{x=\frac{36}{7}}$