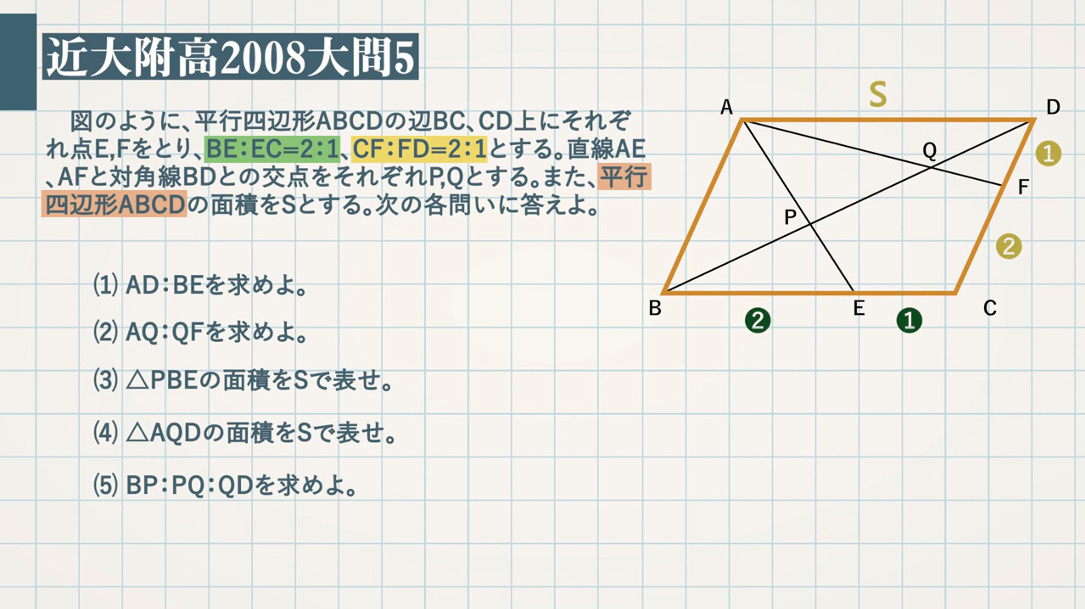
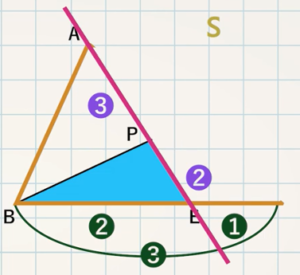
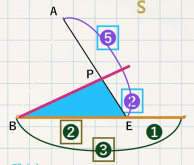
図のように、平行四辺形 $\textcolor{green}{\rm ABCD}$ の辺 $\textcolor{green}{\rm BC}$、$\textcolor{green}{\rm CD}$ 上にそれぞれ点 $\textcolor{green}{\rm E,F}$ をとり、$\textcolor{green}{\rm BE:EC=2:1}$ 、$\textcolor{green}{\rm CF:FD=2:1}$ とする。直線 $\textcolor{green}{\rm AE}$、$\textcolor{green}{\rm AF}$ と対角線 $\textcolor{green}{\rm BD}$ との交点をそれぞれ $\textcolor{green}{\rm P,Q}$ とする。また、平行四辺形 $\textcolor{green}{\rm ABCD}$ の面積を $\textcolor{green}{\rm S}$ とする。次の各問いに答えよ。

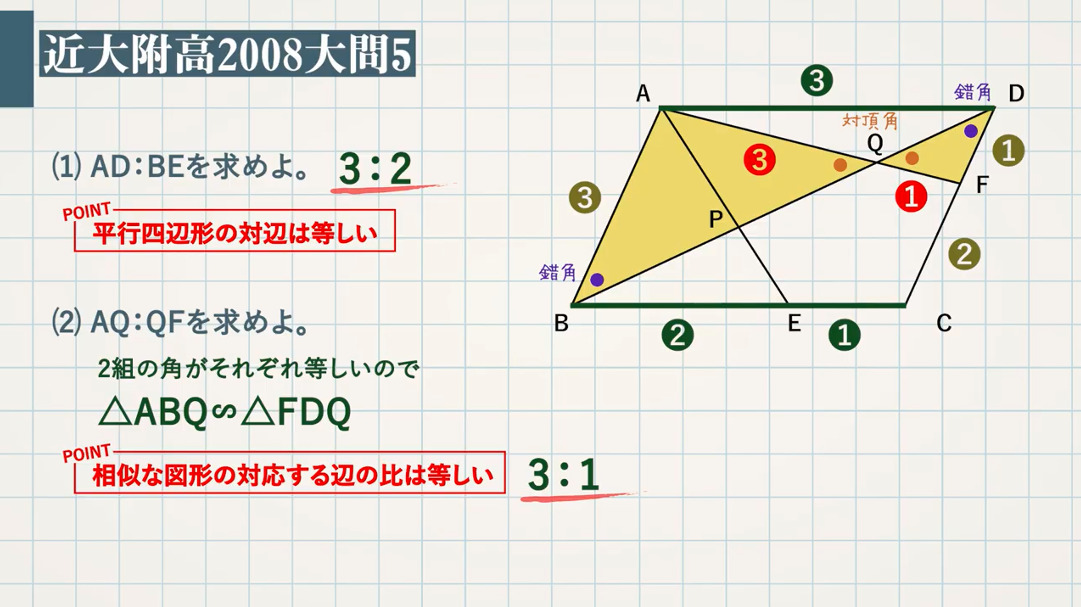
(1) $\textcolor{green}{\rm AD:BE}$ を求めよ。

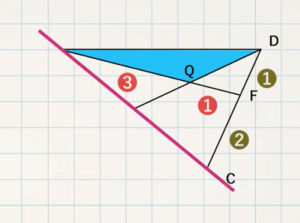
(2) $\textcolor{green}{\rm AQ:QF}$ を求めよ。

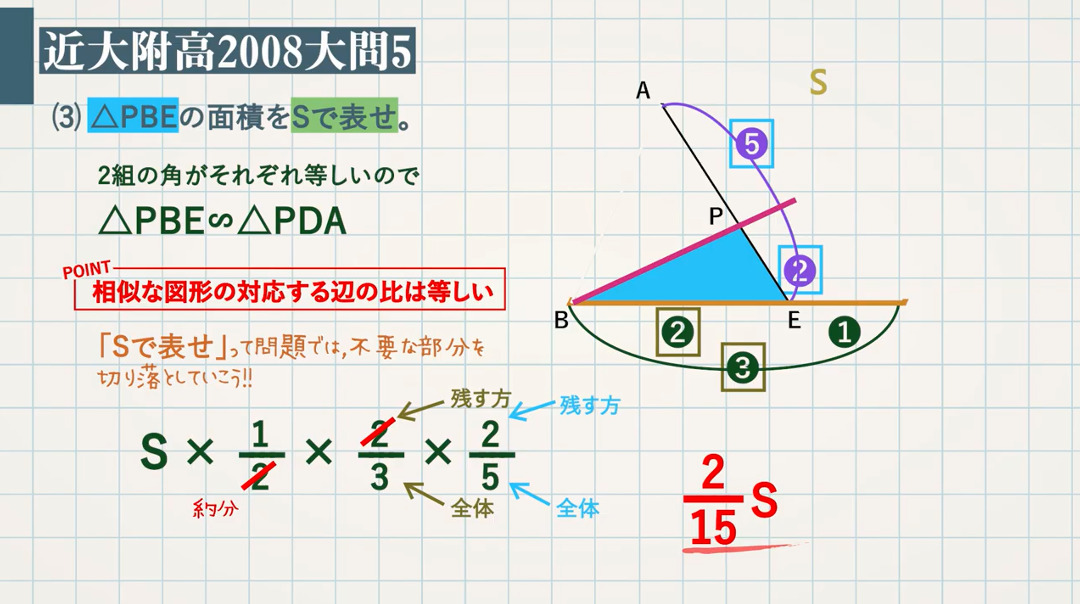
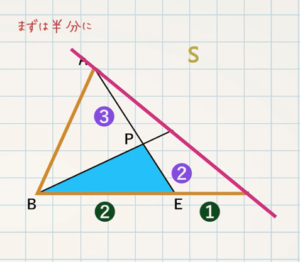
(3) $\textcolor{green}{\rm △PBE}$ の面積を $\textcolor{green}{\rm S}$ で表せ。

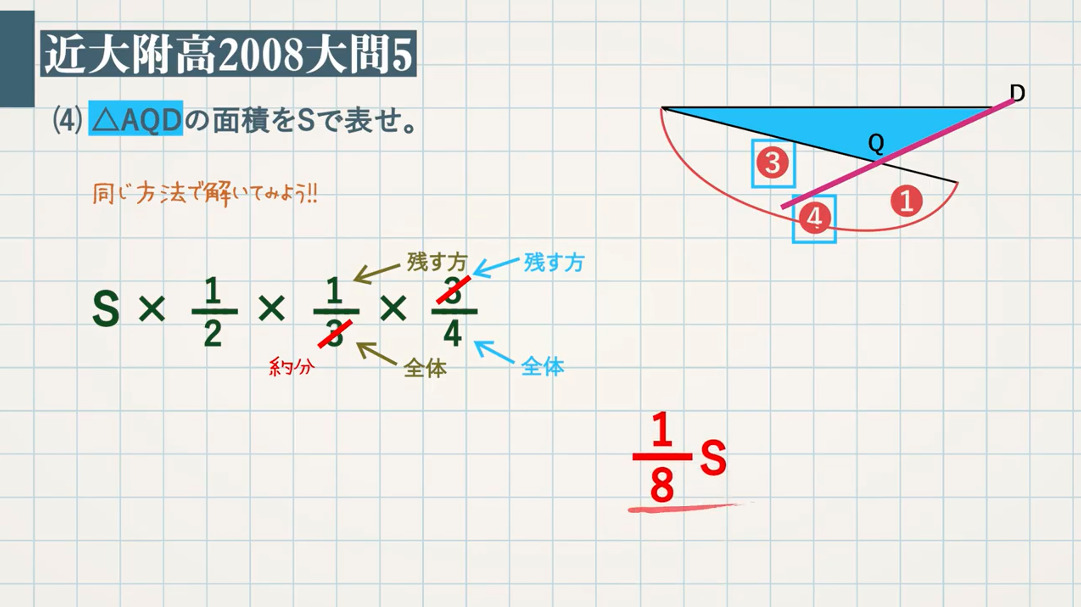
(4) $\textcolor{green}{\rm △AQD}$ の面積を $\textcolor{green}{\rm S}$ で表せ。

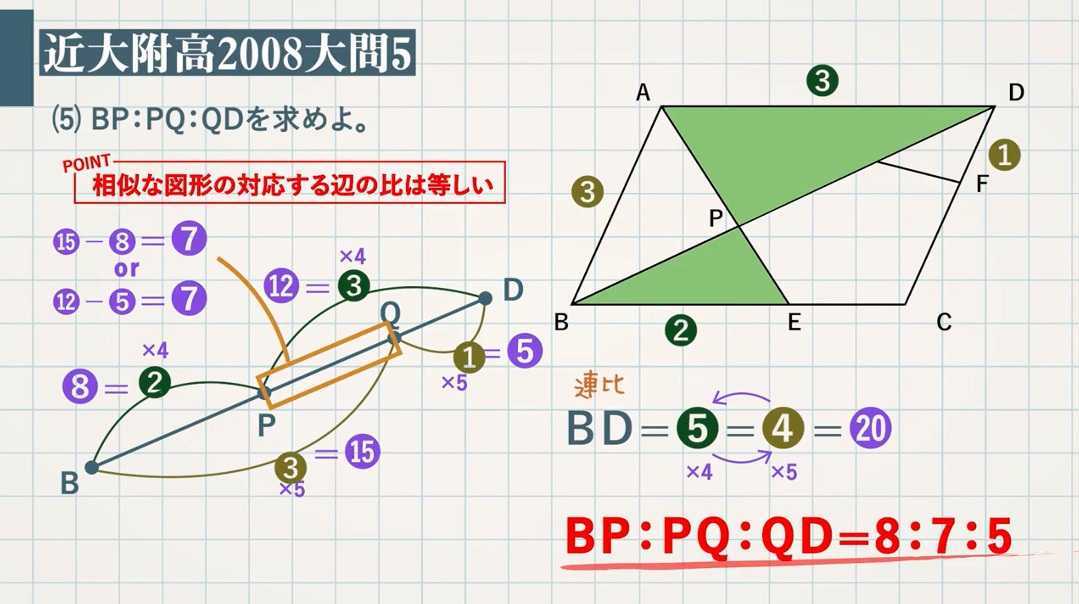
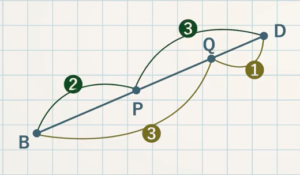
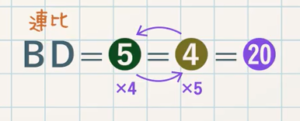
(5) $\textcolor{green}{\rm BP:PQ:QD}$ を求めよ。

一問ずつみていきましょう。

(1) $\textcolor{green}{\rm AD:BE}$ を求めよ。

POINT：平行四辺形の対辺は等しい

$\rm BE:EC=2:1$ より、$\rm AD:BE=\textcolor{red}{3:2}$

(2) $\textcolor{green}{\rm AQ:QF}$ を求めよ。

図の対頂角、錯角の $2$ 組の角がそれぞれ等しいので、$\textcolor{blue}{\rm △ABQ∽△FDQ}$

POINT：相似な図形の対応する辺の比は等しい

$\rm AB:FD=3:1$ より、$\rm AQ:FQ=\textcolor{red}{3:1}$

(3) $\textcolor{green}{\rm △PBE}$ の面積を $\textcolor{green}{\rm S}$ で表せ。

$2$ 組の角がそれぞれ等しいので、$\textcolor{blue}{\rm △PBE∽△PDA}$ 

POINT：相似な図形の対応する辺の比は等しい

「$\rm S$ で表せ」という問題では、不要な部分を切り落としていきましょう。

まずは半分に。$\rm S×\frac{1}{2}=\textcolor{blue}{\frac{1}{2}S}$

$\rm BE:EC=2:1$ より、$\rm \frac{1}{2}S×\frac{2}{3}=\textcolor{blue}{\frac{1}{3}S}$

$\rm AP:PE=3:2$ より、$\rm \frac{1}{3}S×\frac{2}{5}=\textcolor{red}{\frac{2}{15}S}$

　→　　→　

(4) $\textcolor{green}{\rm △AQD}$ の面積を $\textcolor{green}{\rm S}$ で表せ。

(3) と同じ方法で解いてみましょう。

まずは半分に。$\rm S×\frac{1}{2}=\textcolor{blue}{\frac{1}{2}S}$

$\rm CF:FD=2:1$ より、$\rm \frac{1}{2}S×\frac{1}{3}=\textcolor{blue}{\frac{1}{6}S}$

最後に $\rm AQ:QF=3:1$ より、$\rm \frac{1}{6}S×\frac{3}{4}=\textcolor{red}{\frac{1}{8}S}$

　→　　→　

(5) $\textcolor{green}{\rm BP:PQ:QD}$ を求めよ。

POINT：相似な図形の対応する辺の比は等しい

$\rm △AQB∽△FQD$ より、 $\rm BD=BQ+QD=3+1＝\textcolor{blue}{4}$

$\rm △APD∽△EPB$ より、$\rm BD=BP+PD=2+3=\textcolor{blue}{5}$

$\rm PQ=15-8$ or $12-5$ $=\textcolor{blue}{7}$

よって、$\rm BP:PQ:QD=\textcolor{red}{8:7:5}$