相似比（辺の長さの比）から面積比と体積比を求めましょう。

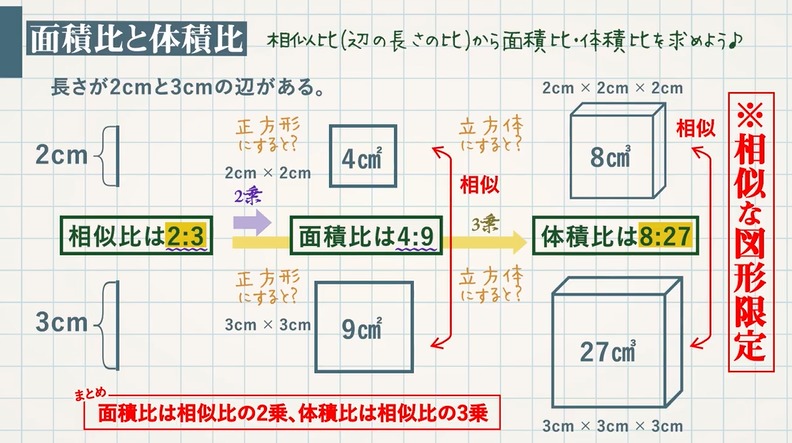
長さ $2\rm cm$ と $3\rm cm$ の辺があります。この $2$ 辺の長さの比（相似比）は $\textcolor{blue}{2:3}$ になります。

正方形にしてそれぞれの面積を考えると、

$1$ 辺の長さが $2 \rm cm:2×2（2\textcolor{blue}
{^2}）=\textcolor{blue}{4\rm cm^2}$ 

$1$ 辺の長さが $3 \rm cm:3×3（3\textcolor{blue}{^2}）=\textcolor{blue}{9\rm cm^2} $

よって、面積比は $\textcolor{blue}{4:9}$

立方体にしてそれぞれの体積を考えると、

$1$ 辺の長さが $2 \rm cm:2×2×2（2\textcolor{blue}{^3}）=\textcolor{blue}{8\rm cm^3} $

$1$ 辺の長さが $3 \rm cm:3×3×3（\textcolor{blue}{3^3}）=\textcolor{blue}{27\rm cm^3} $

よって、体積比は $\textcolor{blue}{8:27}$

POINT:面積比は相似比の $\textcolor{blue}{2}$ 乗、体積比は相似比の $\textcolor{blue}{3}$ 乗となります。

【例題 $\textcolor{green}{1}$ 】平行四辺形 $\textcolor{green}{\rm ABCD}$ で、$\textcolor{green}{\rm AF:DF=2:3}$ であるとき、次の問いに答えなさい。

(1) $\textcolor{green}{\rm △AEF}$ と $\textcolor{green}{\rm △DCF}$ の面積比を求めなさい。

$\rm △AEF$ と $\rm △DCF$ において、

平行線の錯角は等しいので、$\textcolor{blue}{\rm ∠EAF=∠CDF}$…①

対頂角は等しいので、$\textcolor{blue}{\rm  ∠AFE=∠DFC}$…②

①,②より $2$ 組の角がそれぞれ等しいので、$\textcolor{blue}{\rm △AEF∽△DCF}$

$\textcolor{blue}{\rm AF:DF=2:3}$ より、相似比は $\textcolor{blue}{2:3}$

よって、面積比はその$2$ 乗の $\textcolor{red}{4:9}$ となる。

(2) $\textcolor{green}{\rm △DCF}$ の面積は平行四辺形 $\textcolor{green}{\rm ABCD}$ の何倍か求めなさい。

$\rm △DCF$ と平行四辺形 $\rm ABCD$ は、どちらも高さ $\textcolor{blue}{h}$ で同じです。 また、底辺の長さの比は $\rm AF:DF=2:3$ より、$\textcolor{blue}{\rm FD:AD=3:5}$ となります。

${\rm △DCF=}③×h×\frac{1}{2}=\textcolor{blue}{\frac{③}{2}h}×2=\textcolor{blue}{③h}$

平行四辺形 ${\rm ABCD=}⑤×h=\textcolor{blue}{⑤h}×2=\textcolor{blue}{⑩h}$

よって、$\textcolor{red}{\rm △DCF}$ の面積は平行四辺形 $\textcolor{red}{\rm ABCD}$ の $\textcolor{red}{\frac{3}{10}}$ 倍 

【例題 $\textcolor{green}{1}$ 】円すいを底面に平行で高さを $\textcolor{green}{3}$ 等分する $\textcolor{green}{2}$ つの平面で切り分けたとき、立体 $\textcolor{green}{\rm P,Q,R}$ の体積の比を求めなさい。

高さを $3$ 等分と考えると、相似な円すいが $\textcolor{blue}{3}$ つできます。

これは立体$\rm P,Q,R$ でないので要注意です。$3$ つの立体は、

$\textcolor{blue}{\rm P}$：水色の円すい

$\textcolor{blue}{\rm Q}$：オレンジの円すい $\textcolor{blue}{-}$ 水色の円すい

$\textcolor{blue}{\rm R}$：緑の円すい $\textcolor{blue}{-}$ オレンジの円すい

これより、それぞれの体積比（相似比の $\textcolor{blue}{3}$ 乗）を考えると、

立体 $\rm P$ (水色)：$1^3=\textcolor{blue}{1}$

立体 $\rm Q$ (オレンジ $-$ 水色)：$2^3-1^3=\textcolor{blue}{7}$

立体 $\rm Q$ (緑 $-$ オレンジ)：$3^3-2^3=\textcolor{blue}{19}$

よって、立体${\rm P,Q,R}$ の体積の比は $\textcolor{red}{\rm P:Q:R=1:7:19}$