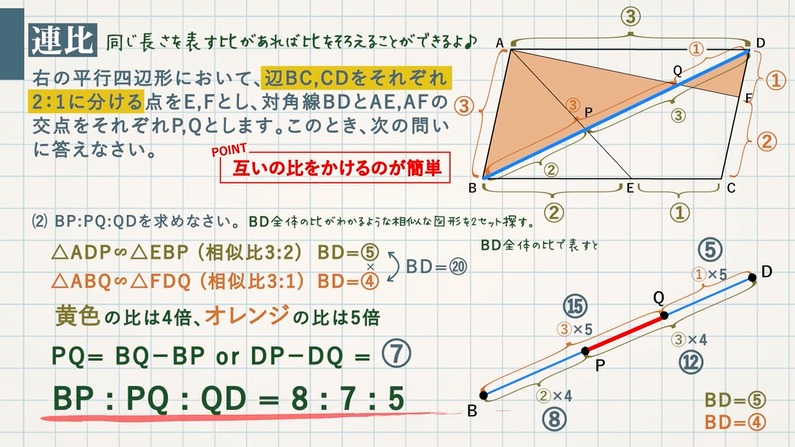
【例題】図の平行四辺形において、辺 $\textcolor{green}{\rm BC,CD}$ をそれぞれ $\textcolor{green}{2:1}$ に分ける点を $\textcolor{green}{\rm E,F}$ とし、対角線 $\textcolor{green}{\rm BD}$ と $\textcolor{green}{\rm AE,AF}$ の交点をそれぞれ $\textcolor{green}{\rm P,Q}$ とします。このとき、次の問いに答えなさい。

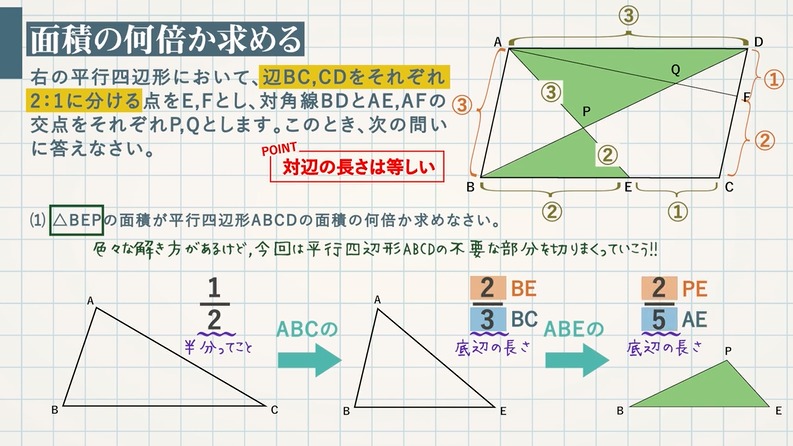
(1) $\textcolor{green}{\rm △BEP}$ の面積が平行四辺形 $\textcolor{green}{\rm ABCD}$ の面積の何倍か求めなさい。

色々な解き方があるけど、今回は平行四辺形 $\rm ABCD$ の不要な部分を切り取っていく。

対角線 $\rm AC$ をひく。

$\rm △ABC$ は平行四辺形 $\rm ABCD$ の半分 $\textcolor{blue}{\frac{1}{2}}$

　$↓$

$\rm △ABE$ は $\rm △ABC$ の $\textcolor{blue}{\frac{2}{3}}$（$\rm \frac{BE}{BC}$）

　$↓$

$\rm △PBE$ は $\rm △ABE$ の $\textcolor{blue}{\frac{2}{5}}$（$\rm \frac{PE}{AE}$）

あとはかけるだけ。$\frac{1}{2}×\frac{2}{3}×\frac{2}{5}=\textcolor{red}{\frac{2}{15}}$ 倍

(2) $\textcolor{green}{\rm BP:PQ:QD}$ を求めなさい。

$\rm BD$ 全体の比がわかるような相似な図形を $2$ セット探す。

$\rm △ADP∽△EBP$（相似比 $3:2$）$\textcolor{blue}{\rm BD=5（3+2）}$

$\rm △ABQ∽△FDQ$（相似比 $3:1$）$\textcolor{blue}{\rm BD=4（3+1）}$

同じ長さ( 今回は $\rm BD$ )を表す比があれば比をそろえることができます。

POINT:互いの比をかけるのが簡単

黄色の比は $4$ 倍、オレンジの比は $5$ 倍

$\textcolor{blue}{\rm BP=⑧（②×4）}$

$\textcolor{blue}{\rm QD=⑤（①×5）}$

$\textcolor{blue}{\rm PQ=BQ-BP}$ or $\textcolor{blue}{\rm DP-DQ=⑦（⑮-⑧}$ or $\textcolor{blue}{⑫-⑤）}$

よって、$\rm BP:PQ:QD=\textcolor{red}{8:7:5}$