まずは中点連結定理のおさらいをしておきましょう。
\begin{eqnarray} \textcolor{blue}{中点連結定理:}\textcolor{blue}{\rm MN=\frac{1}{2}BC} , \textcolor{blue}{\rm MN//BC}\end{eqnarray}
それぞれの中点 $2$ つを結んだら、長さが半分で、平行になります。
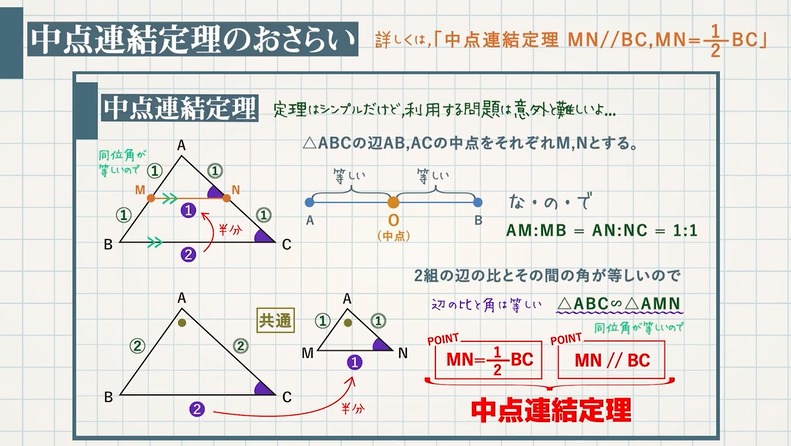
まずは中点連結定理のおさらいをしておきましょう。
\begin{eqnarray} \textcolor{blue}{中点連結定理:}\textcolor{blue}{\rm MN=\frac{1}{2}BC} , \textcolor{blue}{\rm MN//BC}\end{eqnarray}
それぞれの中点 $2$ つを結んだら、長さが半分で、平行になります。
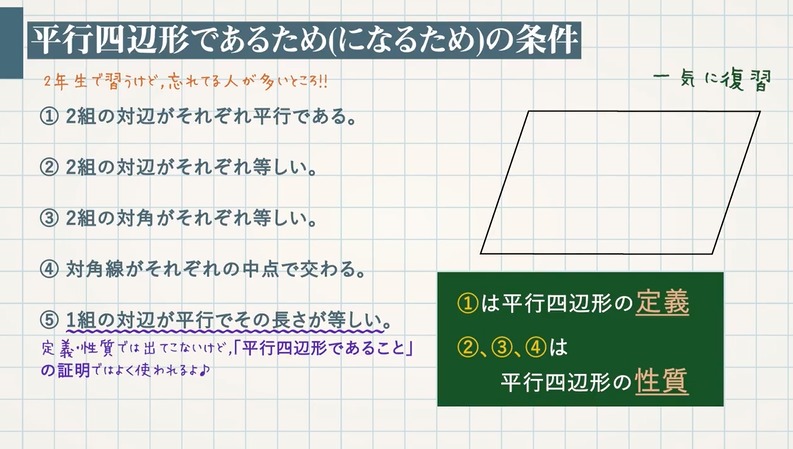
続いて、中学 $2$ 年生で習う平行四辺形であるため(になるため)の条件についても一気に復習しておきましょう。
① $\textcolor{blue}{2}$ 組の対辺がそれぞれ平行である。
② $\textcolor{blue}{2}$ 組の対辺がそれぞれ等しい。
③ $\textcolor{blue}{2}$ 組の対角がそれぞれ等しい。
④ 対角線がそれぞれの中点で交わる
⑤ $\textcolor{blue}{1}$ 組の対辺が平行でその長さが等しい
→定義・性質では出てこないけど、「平行四辺形であること」の証明ではよく使われます。
①は平行四辺形の定義
②、③、④は平行四辺形の性質
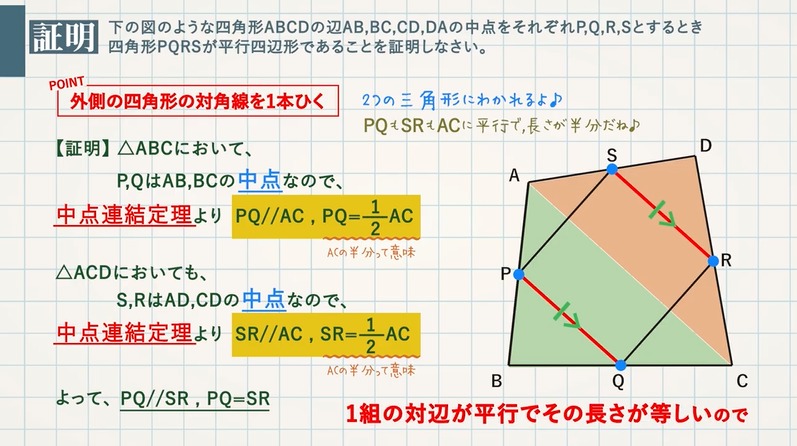
【証明】図のような四角形 $\textcolor{green}{\rm ABCD}$ の辺 $\textcolor{green}{\rm AB,BC,CD,DA}$ の中点をそれぞれ $\textcolor{green}{\rm P,Q,R,S}$ とするとき、四角形 $\textcolor{green}{\rm PQRS}$ が平行四辺形であることを証明しなさい。
POINT:外側の四角形の対角線を $\textcolor{blue}{1}$ 本ひく
【証明】$\rm △ABC$ において、$\rm P,Q$ は$\rm AB,BC$ の中点なので、
中点連結定理より $\textcolor{blue}{\rm PQ//AC, PQ=\frac{1}{2}AC}$
$\rm △ACD$ においても、$\rm S,R$ は $\rm AD,CD$ の中点なので、
中点連結定理より $\textcolor{blue}{\rm SR//AC,SR=\frac{1}{2}AC}$
よって、$\textcolor{blue}{\rm PQ//SR,PQ=SR}$
$\textcolor{blue}{1}$ 組の対辺が平行でその長さが等しいので、四角形PQRSは平行四辺形である。
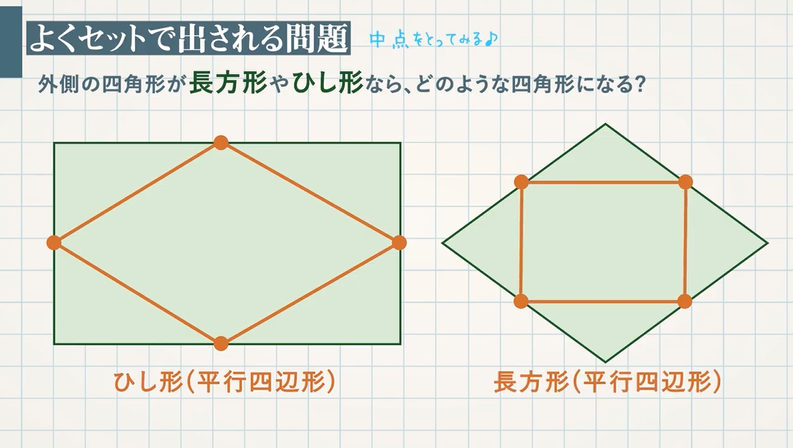
よくセットで出される問題
【例題】次の四角形の各辺の中点を結んでできる四角形はどのような四角形になるか答えなさい。
長方形→ひし形(平行四辺形)
ひし形→長方形(平行四辺形)
コンテンツやシステムに関するお問い合わせ・オファーはこちらから