円に接す線を接線、接する点を接点といいます。

POINT：接線は、接点を通る半径に垂直

図の $\rm AO$ を結ぶと $2$ つのことがわかります。

「円周角の定理の逆」から

POINT： $\textcolor{blue}{2}$ つの接点は、$\textcolor{blue}{\rm AO}$ を直径とする円周上にある。

直角三角形の合同条件「斜辺と他の一辺がそれぞれ等しい」より、上下 $2$ つの三角形は合同なので、

POINT：外部にある点 ($\textcolor{blue}{\rm A}$)から、ひいた $\textcolor{blue}{2}$ 本の接線の長さは等しい

【例題 $\textcolor{green}{1}$ (作図)】円外の点 $\textcolor{green}{\rm A}$ から円 $\textcolor{green}{\rm O}$ に接線をひくとき、接点 $\textcolor{green}{\rm P,Q}$ を作図しなさい。

POINT： $\textcolor{blue}{2}$ つの接点は、$\textcolor{blue}{\rm AO}$ を直径とする円周上にある。

つまり、$\rm AO$ を直径とする円をかけばいいので、

Step $\textcolor{blue}{1}$：円の中心($\textcolor{blue}{\rm AO}$ の中点)を作図する（$\textcolor{blue}{\rm AO}$ の垂直二等分線）

Step $\textcolor{blue}{2}$：円の中心から $\textcolor{blue}{\rm A}$ までを半径とする円をかく

Step $\textcolor{blue}{3}$：円 $\textcolor{blue}{\rm O}$ との交点に点 $\textcolor{blue}{\rm P,Q}$ をかく

Step $\textcolor{blue}{4}$：$\textcolor{blue}{\rm A}$と$\textcolor{blue}{\rm P}$ , $\textcolor{blue}{\rm A}$ と $\textcolor{blue}{\rm Q}$ を結ぶ

※問題が接線の作図ならば、$\rm A$と$\rm P$ , $\rm A$ と $\rm Q$ を通る直線をかきます。

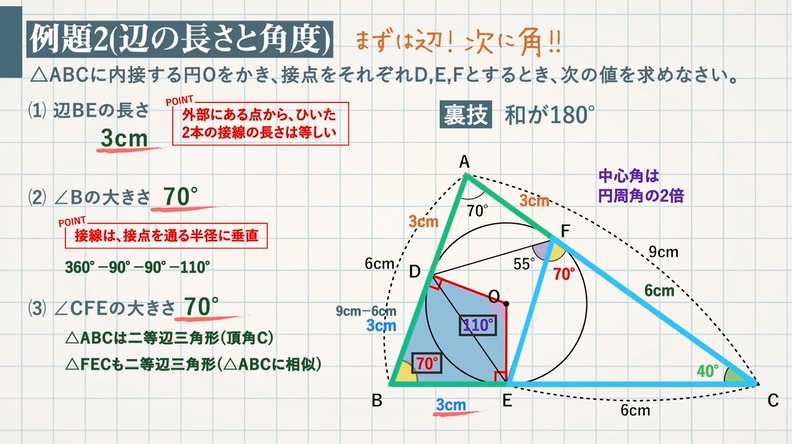
【例題 $\textcolor{green}{2}$ (辺の長さと角度)】$\textcolor{green}{\rm △ABC}$ に内接する円 $\textcolor{green}{\rm O}$ をかき、接点をそれぞれ $\textcolor{green}{\rm D,E,F}$ とするとき、次の値を求めなさい。

(1) 辺 $\textcolor{green}{\rm BE}$ の長さ

POINT：外部にある点 ($\textcolor{blue}{\rm A}$)から、ひいた $\textcolor{blue}{2}$ 本の接線の長さは等しい

$\rm CE=CF=6cm$ より、$\rm FA=9-6=3cm$

$\rm FA=AD=3cm$ より、$\rm DB=6-3=3cm$

$\rm DB=BE$ より、辺 $\textcolor{red}{\rm BE=3cm}$

(2) $\textcolor{green}{\rm ∠B}$ の大きさ

POINT：接線は、接点を通る半径に垂直

四角形 $\rm BEOD$ において、$\rm ∠ODB=∠OEB=90°$

また、$\rm ∠DFE$ は $\stackrel{\frown}{\rm DE}$に対する円周角。

中心角である$\rm ∠DOE$ は、 $55×2=110°$

よって、$\rm ∠B=360°-90°-90°-110°=\textcolor{red}{70°}$

(3) $\textcolor{green}{\rm ∠CFE}$ の大きさ

$\rm △ABC$ は二等辺三角形なので、$\rm ∠A=∠B=70°$

また、$\rm △FEC$ も二等辺三角形（$\rm △ABC$ に相似）なので、$\textcolor{red}{\rm ∠CFE=70°}$

【例題 $\textcolor{green}{3}$ (周の長さ)】図で、点 $\textcolor{green}{\rm P,Q,R}$ は円 $\textcolor{green}{\rm O}$ の円周上の点で、辺 $\textcolor{green}{\rm AP,AR,BC}$ は円 $\textcolor{green}{\rm O}$ の接線である。$\textcolor{green}{\rm △ABC}$ の周の長さを求めなさい。

POINT：接線は、接点を通る半径に垂直

接線 $\rm BC$ 上の接点を $\rm M$ とする。

$\rm BO$に線をひき $2$ つの三角形をつくると、

$\textcolor{blue}{\rm △BOP≡△BOM}$ より、$\textcolor{blue}{\rm BP=BM}$

$\textcolor{blue}{\rm AB+BP=AB+BM=7cm}$

同じように $\textcolor{blue}{\rm △COR≡△COM}$ より、$\textcolor{blue}{\rm CR=CM}$

$\textcolor{blue}{\rm AC+CR=AC+CM=7cm}$

よって、$\rm △ABC$ の周の長さは、$\rm 7cm+7cm=\textcolor{red}{14cm}$