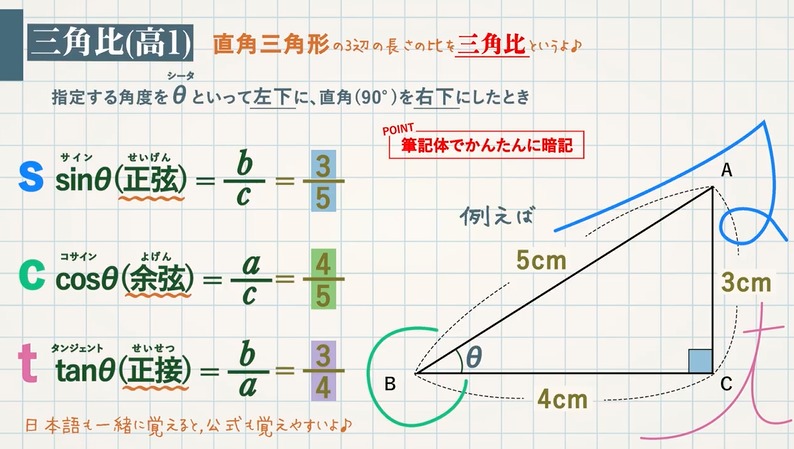
直角三角形の直角をはさむ $2$ 辺の長さを $a,b$ 、斜辺の長さを $c$ とすると、

$\textcolor{blue}{a^2+b^2=c^2}$（短い辺を $\textcolor{blue}{2}$ 乗して足すと斜辺の $\textcolor{blue}{2}$ 乗になる）

これを三平方の定理といいます。

$\rm BC=4cm$ , $\rm AB(斜辺)=5cm$ のとき、$\rm AC$ の長さは、

\begin{eqnarray} 4^2+b^2&=&5^2\\ b^2&=&9\\ b&=&±3\\ \end{eqnarray}

図形の問題なので、マイナスではない。$\textcolor{blue}{b=3}$

注意点：式をつくるときに、斜辺の位置を間違えない。

斜辺 → ①直角に対する辺 ②最も長い辺。

特別な直角三角形は三角定規の $\textcolor{blue}{2}$ 種類になります。

① $\textcolor{blue}{30°,60°,90°}$　POINT：正三角形の半分

正三角形の $1$ 辺の長さを②とすると、$1$ 辺はその半分なので①となります。残り $1$ 辺を三平方の定理を使って求めると、

【三平方の定理】

　$1^2+x^2=2^2$　これを解いて、$\textcolor{blue}{x=\sqrt{3}}$

　よって、その辺の比は、$\textcolor{blue}{1:2:\sqrt{3}}$ となります。

② $\textcolor{blue}{45°,45°,90°}$　POINT：正方形の半分

正方形の $1$ 辺の長さを①とすると、$1$ 辺は同じ長さなので①となります。残り $1$ 辺(斜辺)を三平方の定理を使って求めると、

【三平方の定理】

　$1^2+1^2=x^2$　これを解いて、$\textcolor{blue}{x=\sqrt{2}}$

　よって、その辺の比は、$\textcolor{blue}{1:1:\sqrt{2}}$ となります。

【例題】次の各図の $\textcolor{green}{x}$ を求めなさい。

(1) 三平方の定理 $\textcolor{blue}{a^2+b^2=c^2}$

$\textcolor{blue}{\sqrt{7^2}+x^2=5^2}$　これを解いて、$\textcolor{red}{x=3\sqrt{2}}$

(2) 特別な直角三角形 $\textcolor{blue}{1}$　辺の比 $\textcolor{blue}{1:2:\sqrt{3}}$

$2:\sqrt{3}=8:x$　これを解いて、$\textcolor{red}{x=4\sqrt{3}}$

(3) 特別な直角三角形 $\textcolor{blue}{2}$　辺の比 $\textcolor{blue}{1:1:\sqrt{2}}$

$1:\sqrt{2}=10:x$　これを解いて、$\textcolor{red}{x=10\sqrt{2}}$

直角三角形の $3$ 辺の長さの比を三角比といいます。

指定する角度をθといって左下に、直角を右下にしたとき、(図参照)

\begin{eqnarray} \textcolor{blue}{\rm s　sinθ（正弦）=}\textcolor{blue}{\frac{b}{c}}=\frac{3}{5}\\\\ \textcolor{blue}{\rm c　cosθ（余弦）=}\textcolor{blue}{\frac{a}{c}}=\frac{4}{5}\\\\ \textcolor{blue}{\rm t　tanθ（正接）=}\textcolor{blue}{\frac{b}{c}}=\frac{3}{4}\end{eqnarray}

POINT：筆記体でかんたんに暗記

三角比の表は、特別な直角三角形を考えれば $90°$ までは作ることができます。

【裏技 ($\textcolor{blue}{0°から90°}$) 】

$\textcolor{blue}{\frac{\sqrt{　}}{2}}$ を用意して、ここに数字を入れるだけです。

入れる数字は、$\textcolor{blue}{\rm sinθ}$ → 左から $\textcolor{blue}{0,1,2,3,4}$

　　　　　　　$\textcolor{blue}{\rm cosθ}$ → 左から $\textcolor{blue}{4,3,2,1,0}$

$90°$ を超える場合は？ → 左右対称になります。

ただし、横軸はマイナスなので、$\textcolor{blue}{\rm cosθ,tanθ}$ はマイナスになります。