$\sqrt{7}$ と$\sqrt{11}$ はどちらが大きいのでしょうか。平方根の大小を調べてみましょう。$\sqrt{a}$ は $2$ 乗すると $a$ になる数なので、

$\sqrt{7}$ は面積が $7$ の正方形の $1$ 辺の長さ

$\sqrt{11}$ は面積が $11$ の正方形の $1$ 辺の長さ

となります。よって、$\sqrt{a}$ と $\sqrt{b}$ の大小関係は、

$a,b$ が正の数で $\textcolor{blue}{a＜b}$  ならば $\textcolor{blue}{\sqrt{a}＜\sqrt{b}}$ となります。

次は整数と平方根の大小関係についてみていきましょう。

$\textcolor{green}{5}$ と$\textcolor{green}{\sqrt{23}}$ ではどちらが大きいでしょうか。

これはどちらの数も $\textcolor{blue}{2}$ 乗して比べれば求めることができます。

\begin{eqnarray} 5^2&=&25\\ \sqrt{23^2}&=&23　よって、\textcolor{red}{\sqrt{23}＜5} となります。\end{eqnarray}

今後を考えると、$\sqrt{a}$ の形に変形できた方がいいですね。

$ 5→\sqrt{5^2}→\sqrt{25}$　$\sqrt{23}＜\sqrt{25}$ なので、$\textcolor{red}{\sqrt{23}＜5}$

【問題】数直線の対応する点をそれぞれ答えなさい。

いろいろな解き方がありますが、数直線を $\textcolor{blue}{\sqrt{　}}$ にして考えるのが簡単です。

数直線の各数字を $\sqrt{　}$ に変形すると、$2=\sqrt{2^2}=\sqrt{4}$　,　$3=\sqrt{3^2}=\sqrt{9}$　,　$-1=-\sqrt{1^2}=-\sqrt{1}$　等々

よって、$\sqrt{5}$ は $\textcolor{blue}{2(\sqrt{4})}$ と $\textcolor{blue}{3(\sqrt{9})}$ の間の点なので、E　

$-\sqrt{3}$ は $\textcolor{blue}{-1}$ と $\textcolor{blue}{-2(-\sqrt{4})}$ の間の点なので、 Bとなります。

【問題】$\textcolor{green}{\sqrt{2}＜n＜\sqrt{10}}$ にあてはまる整数 $\textcolor{green}{n}$ は？

この問題も先ほどの数直線の問題と同じく数直線を$\textcolor{blue}{\sqrt{　}}$ にして考えましょう。

\begin{eqnarray} 1&=&\sqrt{1}\\ 2&=&\sqrt{2^2}=\sqrt{4}\\ 3&=&\sqrt{3^2}=\sqrt{9}\\ \end{eqnarray}

以上より、$\sqrt{2}$ から$\sqrt{10}$ の間にある整数は、$\textcolor{blue}{2,3}$　

よって、$\textcolor{red}{n=2,3}$

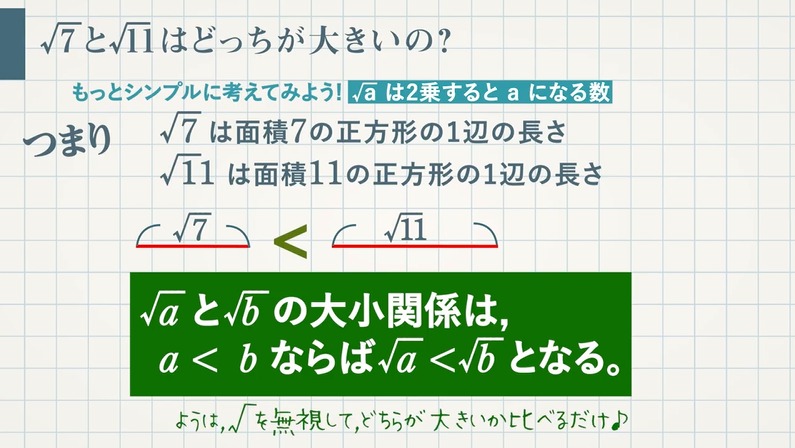
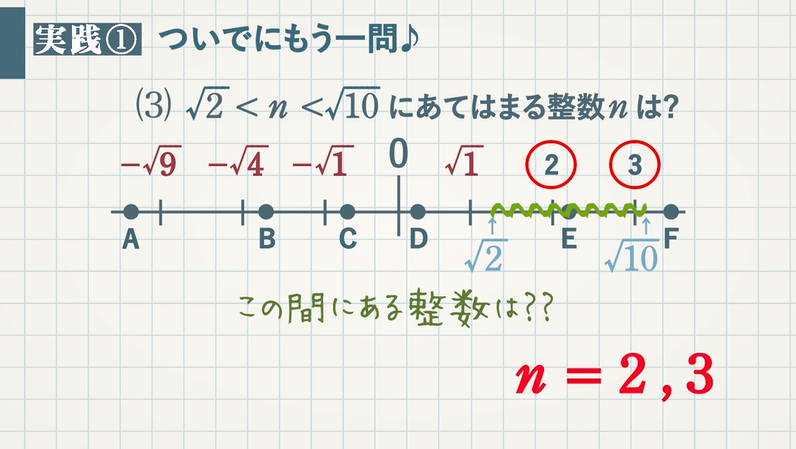
【問題】次の数を小さい方から順に並べなさい。

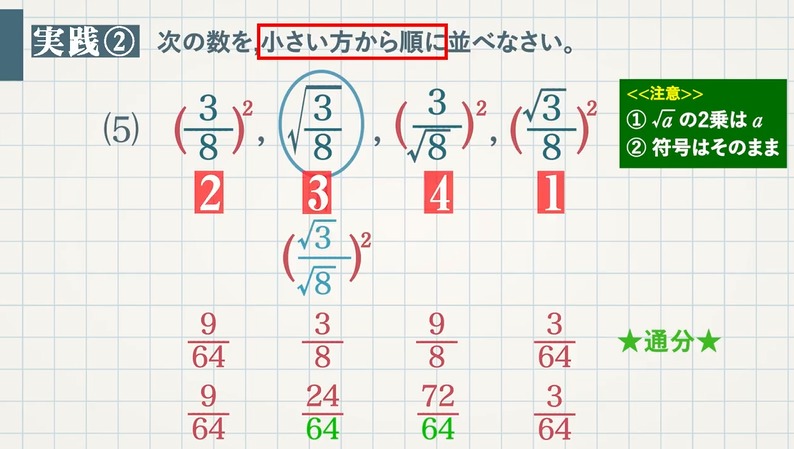
　$\textcolor{green}{\frac{3}{8}}$　,　$\textcolor{green}{\sqrt{\frac{3}{8}}}$　,　$\textcolor{green}{\frac{3}{\sqrt{8}}}$　,　$\textcolor{green}{\frac{\sqrt{3}}{8}}$

それぞれの $\textcolor{blue}{2}$ 乗を比べます。

\begin{eqnarray} (\frac{3}{8})^2&=&\frac{9}{64}=\frac{9}{64}・・・\textcolor{red}{2}\\\\ (\sqrt{\frac{3}{8}})^2&=&\frac{3}{8}=\frac{24}{64}・・・\textcolor{red}{3}\\\\ (\frac{3}{\sqrt{8}})^2&=&\frac{9}{8}=\frac{72}{64}・・・\textcolor{red}{4}\\\\ (\frac{\sqrt{3}}{8})^2&=&\frac{3}{64}=\frac{3}{64}・・・\textcolor{red}{1} \end{eqnarray}

よって、$\textcolor{red}{\frac{\sqrt{3}}{8}}$ → $\textcolor{red}{\frac{3}{8}}$ → $\textcolor{red}{\sqrt{\frac{3}{8}}}$ → $\textcolor{red}{\frac{3}{\sqrt{8}}}$