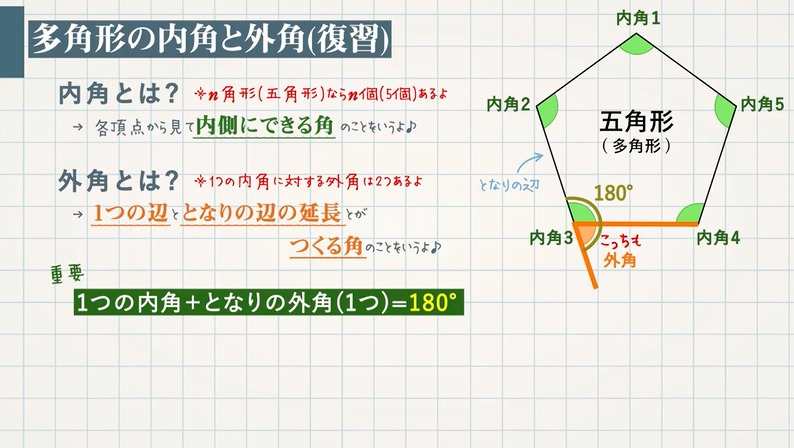
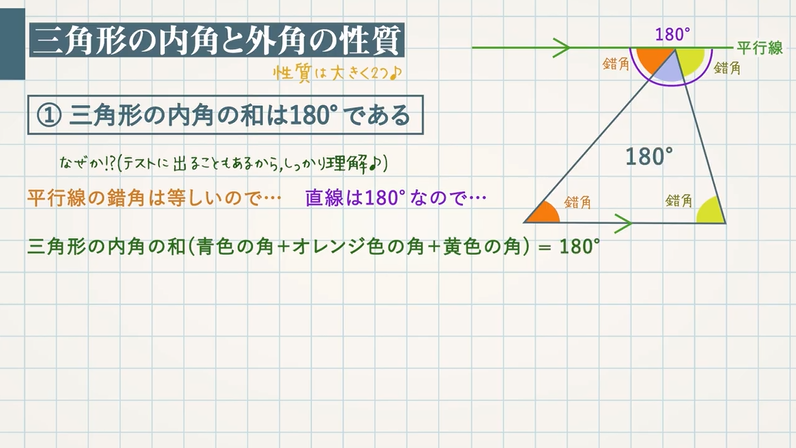
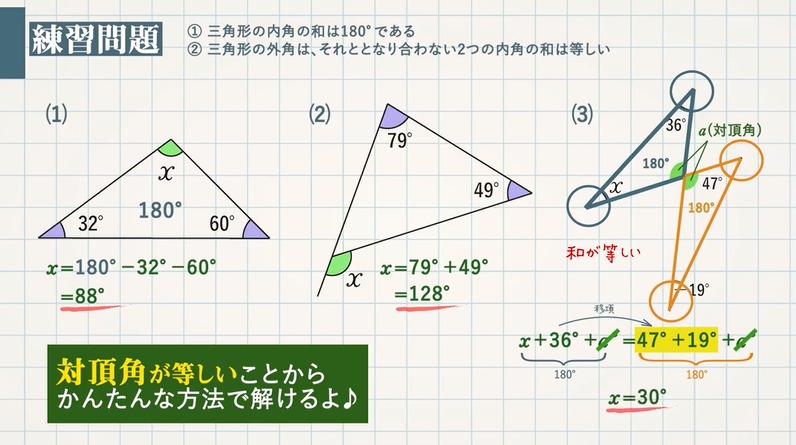
内角とは?
→各頂点から見て内側にできる角のことをいいます。
※ $n$ 角形(五角形)なら内角は $\textcolor{blue}{n}$ 個($\textcolor{blue}{5}$ 個)あります。
外角とは?
→ $\textcolor{blue}{1}$ つの辺ととなりの辺の延長とがつくる角のことをいいます。
※ $1$ つの内角に対する外角は $\textcolor{blue}{2}$ つあります。
重要
$\textcolor{blue}{1}$ つの内角 $\textcolor{blue}{+}$ となりの外角($\textcolor{blue}{1}$ つ)$\textcolor{blue}{=}$ $\textcolor{blue}{180°}$