多角形の内角の和は、$\textcolor{blue}{180°×(n-2)}$ で求めることができます。

図のような六角形の内角の和は？

六角形なので、$n=6$

$180°×(\textcolor{blue}{6}-2)=180°×4=\textcolor{red}{720°}$

なぜ、$180°×(n-2)$ で内角の和が求められるのかについては $\textcolor{blue}{2}$ つの考え方があります。テストにもよく出るので、しっかり理解しましょう。

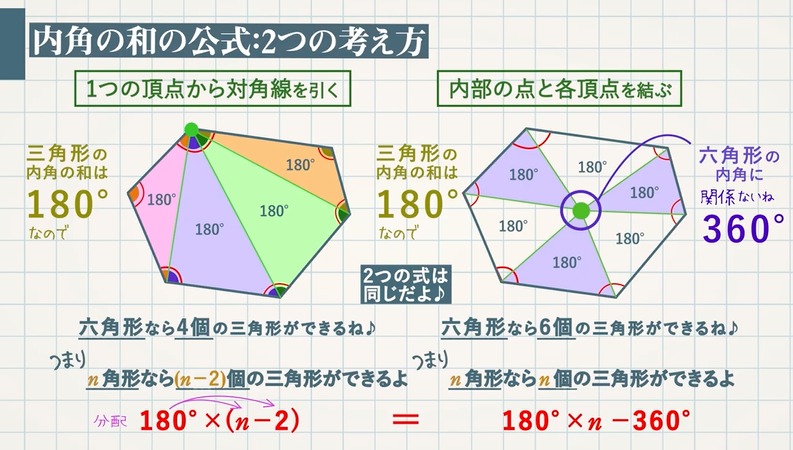
内角の和の公式を導く $2$ つの考え方を確認しましょう。

① $\textcolor{green}{1}$ つの頂点から対角線を引く

対角線を引くと、六角形なら $4$ 個$(6-2 個)$の三角形ができます。

つまり、$\textcolor{blue}{n}$ 角形なら $\textcolor{blue}{(n-2)}$個の三角形ができます。

三角形の内角の和は $180°$ なので、$\textcolor{red}{180°×(n-2)}$

② 内部の点と各頂点を結ぶ

点から各頂点に線を引くと、六角形なら $6$ 個の三角形ができます。

つまり、$\textcolor{blue}{n}$ 角形なら $\textcolor{blue}{n}$ 個の三角形ができます。

三角形の内角の和は $180°$ なので、$\textcolor{blue}{180°×n}$

そこから、六角形の内角に関係ない $\textcolor{blue}{360°}$ を引くので、$\textcolor{red}{180°×n-360°}$

多角形の外角の和は、$\textcolor{blue}{360°}$ となります。

何角形であっても同じ $\textcolor{blue}{360°}$ です。

正三角形の場合を考えてみると、正三角形の $1$ つの内角は $60°$ なので、$1$ つの外角は、$180°-60°=\textcolor{blue}{120°}$ となります。

三角形は外角が $3$ つなので、その和は、$120°×3=\textcolor{red}{360°}$

正四角形の場合でも考えてみると、正四角形の $1$ つの内角は $90°$ なので、$1$ つの外角は、$180°-90°=\textcolor{blue}{90°}$ となります。

四角形は外角が $4$ つなので、その和は、$120°×4=\textcolor{red}{360°}$

【例題(前半)】次の問いに答えなさい。

(1) 十四角形の内角の和を求めなさい。

内角の和 $=\textcolor{blue}{180°×(n-2)}$

$180°×(\textcolor{blue}{14}-2)=180°×12=\textcolor{red}{2160°}$

(2) 二十角形の外角の和を求めなさい。

外角の和は、何角形であっても $\textcolor{red}{360°}$

(3) 内角の和が $\textcolor{green}{1260°}$ である多角形を求めなさい。

内角の和 $=\textcolor{blue}{180°×(n-2)}$

$180°×(n-2)=1260°$　両辺を $180$ でわる

   　　　　$n-2=7$

　　　　　　   $n=\textcolor{blue}{9}$　　　　$\textcolor{red}{9}$ 角形

【例題(後半)】次の問いに答えなさい。

正多角形についての問題は外角で求めた方がかんたんです。

(4) $\textcolor{green}{1}$ つの内角が $\textcolor{green}{135°}$ である正多角形を求めなさい。

$1$ つの内角が $135°$ なので、$1$ つの外角は $45°$ 

外角の和 $360°÷45°=\textcolor{blue}{8}$　　　正八角形

(5) 正十五角形の $\textcolor{green}{1}$ つの内角を求めなさい。

$1$ つの外角は、外角の和 $360°÷15$ 個 $=\textcolor{blue}{24°}$

$1$ つの内角 $180°-24°=\textcolor{red}{156°}$