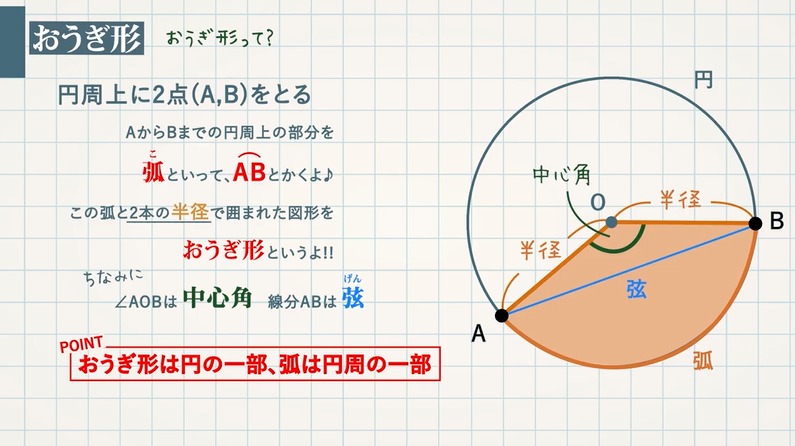
円周上に $2$ 点 ($\rm A,B$) をとる。このとき、$\rm A$ から $\rm B$ までの円周上の部分を弧といって、$\textcolor{blue}{\stackrel{\frown}{\rm AB}}$ とかきます。
この弧と $\textcolor{blue}{2}$ 本の半径で囲まれた図形をおうぎ形といいます。
ちなみに、$\rm ∠AOB$ は中心角といい、線分 $\rm AB$ は弦といいます。
POINT:おうぎ形は円の一部、弧は円周の一部
円周上に $2$ 点 ($\rm A,B$) をとる。このとき、$\rm A$ から $\rm B$ までの円周上の部分を弧といって、$\textcolor{blue}{\stackrel{\frown}{\rm AB}}$ とかきます。
この弧と $\textcolor{blue}{2}$ 本の半径で囲まれた図形をおうぎ形といいます。
ちなみに、$\rm ∠AOB$ は中心角といい、線分 $\rm AB$ は弦といいます。
POINT:おうぎ形は円の一部、弧は円周の一部
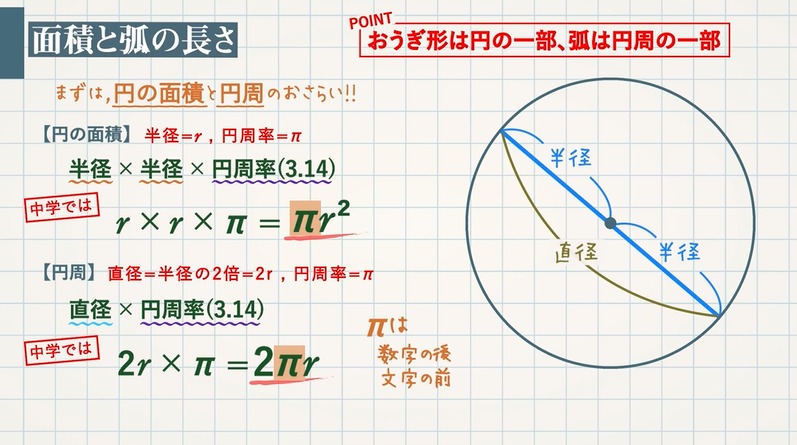
まずは、円の面積と円周の求め方をおさらいしましょう。
【円の面積】
半径 $×$ 半径 $×$ 円周率($3.14$) ですが、中学では、半径 $=$ $r$ , 円周率 $=$ $π$ として、次のように表します。
$\textcolor{blue}{r×r×π=πr^2}$
【円周】
直径 $×$ 円周率($3.14$) ですが、中学では、半径 $=$ $r$ , 円周率 $=$ $π$ として、次のように表します。
$\textcolor{blue}{2×r×π=2πr}$
※ $\textcolor{blue}{π}$ をかく順番は数字の後、文字の前になります。

続いてはおうぎ形の面積と弧の長さです。
POINT:おうぎ形は円の一部、弧は円周の一部
なので、円の $\frac{〇}{〇}$ か考えます。 例えば、
\begin{eqnarray} 黄色のおうぎ形:\frac{中心角}{ 360°}=\frac{180°}{360°}=\textcolor{blue}{\frac{1}{2}}\\\\ 緑色のおうぎ形:\frac{中心角}{ 360°}=\frac{90°}{360°}=\textcolor{blue}{\frac{1}{4}}\end{eqnarray}
よって、おうぎ形の面積と弧の長さは以下のように求めることができます。
\begin{eqnarray} &\textcolor{blue}{【}&\textcolor{blue}{おうぎ形の面積】} \textcolor{blue}{πr^2×\frac{中心角}{360°}}\\\\ &\textcolor{blue}{【}&\textcolor{blue}{おうぎ形の弧の長さ】} \textcolor{blue}{2πr×\frac{中心角}{360°}}\end{eqnarray}

【例題(基礎)】次のおうぎ形の面積と弧の長さを求めなさい。
(1) 半径 $\textcolor{green}{=4\rm cm}$ , 中心角 $\textcolor{green}{=45°}$
\begin{eqnarray} \textcolor{blue}{【面積】半径×半径×π×\frac{中心角}{360°}}\\ 4×4×π×\frac{45°}{360°}=\textcolor{red}{2π (\rm cm^2)}\\ \textcolor{blue}{【弧の長さ】2×半径×π×\frac{中心角}{360°}}\\ 2×4×π×\frac{45°}{360°}=\textcolor{red}{π (\rm cm)}\end{eqnarray}
(2) 半径 $\textcolor{green}{=4\rm cm}$ , 中心角 $\textcolor{green}{=216°}$ \begin{eqnarray} \textcolor{blue}{【面積】半径×半径×π×\frac{中心角}{360°}}\\ 10×10×π×\frac{216°}{360°}=\textcolor{red}{60π (\rm cm^2)}\\ \textcolor{blue}{【弧の長さ】2×半径×π×\frac{中心角}{360°}}\\ 2×10×π×\frac{216°}{360°}=\textcolor{red}{12π (\rm cm)}\end{eqnarray}
【例題(応用)】次の問いに答えなさい。
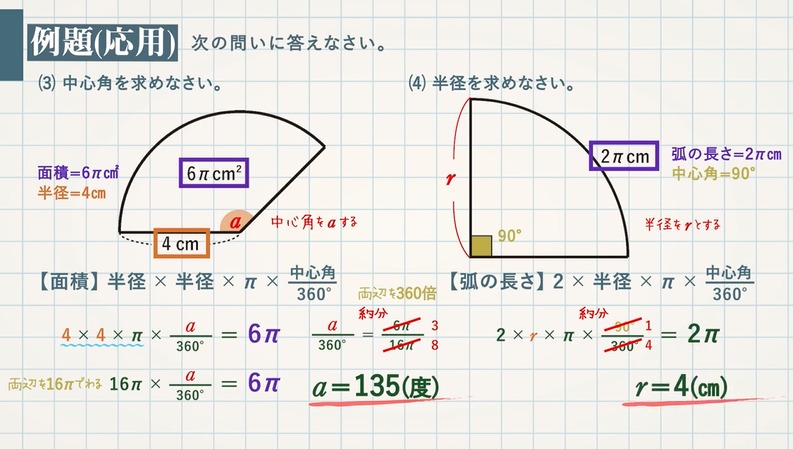
(3) 中心角を求めなさい。面積$\textcolor{green}{=6π\rm cm^2}$ , 半径 $\textcolor{green}{=4\rm cm}$
\begin{eqnarray}& &\textcolor{blue}{【面積】半径×半径×π×\frac{中心角}{360°}}\\& & 4×4×π×\frac{a}{360°}=6π\\& &これを解いて、\textcolor{red}{a=135(度)}\end{eqnarray}
(4) 半径を求めなさい。弧の長さ $\textcolor{green}{=2π\rm cm}$ , 中心角 $\textcolor{green}{=90°}$
\begin{eqnarray}& & \textcolor{blue}{【弧の長さ】2×半径×π×\frac{中心角}{360°}}\\& &
2×r×π×\frac{90°}{360°}=2π \\& &これを解いて、\textcolor{red}{r=4(\rm cm)}\end{eqnarray}
コンテンツやシステムに関するお問い合わせ・オファーはこちらから