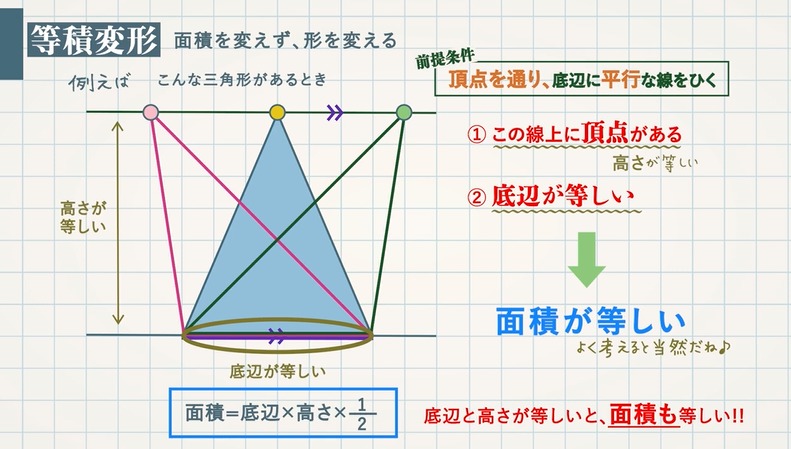
等積変形：面積を変えず、形を変える

前提条件：頂点を通り、底辺に平行な線をひく

①この線上に頂点がある（高さが等しい）

②底辺が等しい

　　$↓$

面積が等しい

三角形の面積は、$\textcolor{blue}{面積=底辺×高さ×\frac{1}{2}}$ なので、

底辺と高さが等しいと、面積も等しくなります。

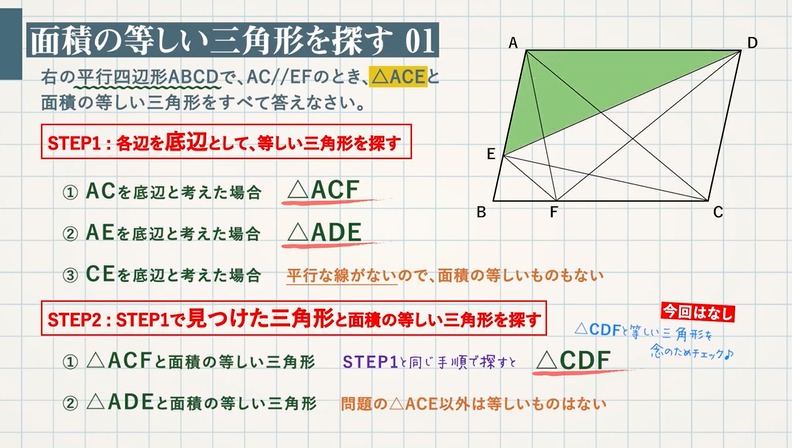
【例題 $\textcolor{green}{1}$ 】右の平行四辺形 $\textcolor{green}{\rm ABCD}$ で、$\textcolor{green}{\rm AC//EF}$ のとき、$\textcolor{green}{\rm △ACE}$ と面積の等しい三角形をすべて答えなさい。

STEP $\textcolor{blue}{1}$：各辺を底辺として、等しい三角形を探す

① $\rm AC$を底辺と考えた場合　$\rm AC//EF$ より、$\textcolor{blue}{\rm △ACF}$

② $\rm AE$を底辺と考えた場合　 $\rm AE//DC$ より、$\textcolor{blue}{\rm △ADE}$

③ $\rm CE$ を底辺と考えた場合　平行な線がないので、面積の等しいものもない

STEP $\textcolor{blue}{2}$：STEP $\textcolor{blue}{1}$ で見つけた三角形と面積の等しい三角形を探す

① $\rm △ACF$ と面積の等しい三角形　$\textcolor{blue}{\rm △CDF}$

※ $\rm △CDF$ と等しい三角形を念のためにチェック→今回はなし

② $\rm △ADE$ と面積の等しい三角形　問題の $\textcolor{blue}{\rm △ACE}$ 以外は等しいものはない

よって、$\rm △ACE$ と面積の等しい三角形は、$\textcolor{red}{\rm △ACF,△ADE,△CDF}$

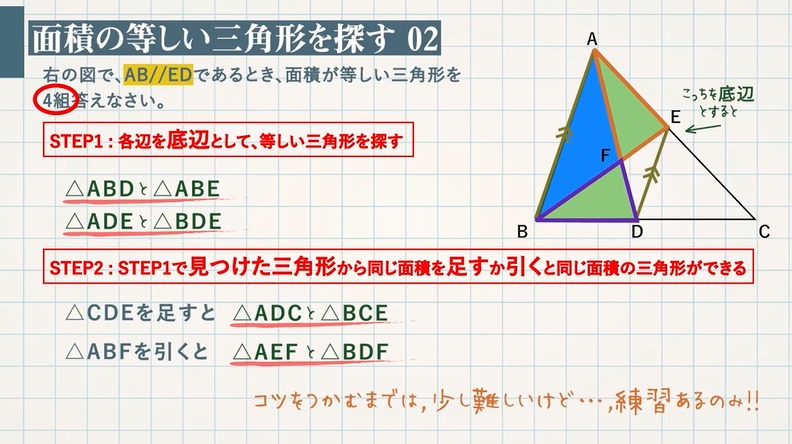
【例題 $\textcolor{green}{2}$ 】右の図で、$\textcolor{green}{\rm AB//ED}$ であるとき、面積が等しい三角形を $\textcolor{green}{4}$ 組答えなさい。

STEP $\textcolor{blue}{1}$：各辺を底辺として、等しい三角形を探す

$\textcolor{blue}{\rm AB//ED}$ より、

① $\rm AB$ を底辺とすると、$\textcolor{blue}{\rm △ABD}$ と $\textcolor{blue}{\rm △ABE}$

② $\rm DE$ を底辺とすると、$\textcolor{blue}{\rm △ADE}$ と $\textcolor{blue}{\rm △BDE}$

STEP $\textcolor{blue}{2}$：STEP $\textcolor{blue}{1}$ で見つけた三角形から同じ面積を足すか引くと同じ面積の三角形ができる

$\rm △ADE$ , $\rm △BDE$ に $\textcolor{blue}{\rm △CDE}$ を足すと、

$\textcolor{blue}{\rm △ADC}$ と $\textcolor{blue}{\rm △BCE}$

$\rm △ABD$ , $\rm △ABE$ から $\textcolor{blue}{\rm △ABF}$ を引くと、

$\textcolor{blue}{\rm △BDF}$ と $\textcolor{blue}{\rm △AEF}$

よって、面積が等しい三角形 $4$ 組は、

$\textcolor{red}{\rm △ABD}$ と $\textcolor{red}{\rm △ABE}$  $,$  $\textcolor{red}{\rm △ADE}$ と $\textcolor{red}{\rm △BDE}$

$\textcolor{red}{\rm △ADC}$ と $\textcolor{red}{\rm △BCE}$  $,$  $\textcolor{red}{\rm △AEF}$ と $\textcolor{red}{\rm △BDF}$