まずは立体の体積を求める公式を確認しましょう。
【角柱・円柱】 底面積 $\textcolor{blue}{×}$ 高さ
【角錐・円錐】 底面積 $×$ 高さ$\textcolor{blue}{×\frac{1}{3}}$
【球】 $\textcolor{blue}{\frac{4}{3}×π×r^3}$
$3$ 種類の公式を使い、いろいろな立体の体積を求めてみましょう。

まずは立体の体積を求める公式を確認しましょう。
【角柱・円柱】 底面積 $\textcolor{blue}{×}$ 高さ
【角錐・円錐】 底面積 $×$ 高さ$\textcolor{blue}{×\frac{1}{3}}$
【球】 $\textcolor{blue}{\frac{4}{3}×π×r^3}$
$3$ 種類の公式を使い、いろいろな立体の体積を求めてみましょう。
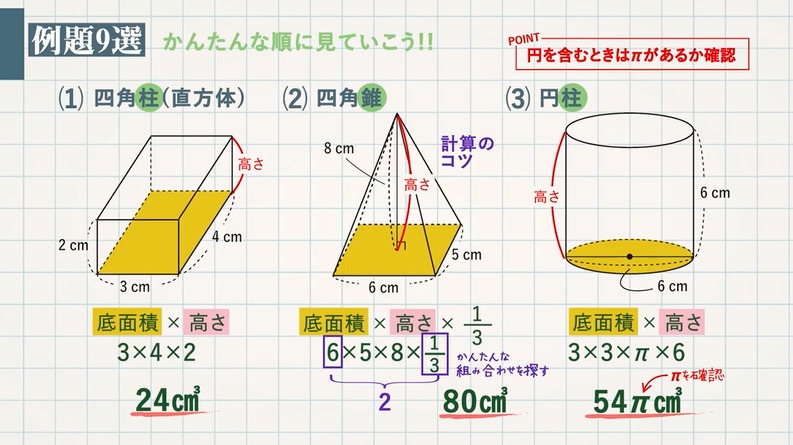
(1) 四角柱(直方体)
底面積 $\textcolor{blue}{×}$ 高さ $3×4$ $×$ $2$ $=\textcolor{red}{\rm 24cm^3}$
(2) 四角錐
底面積 $\textcolor{blue}{×}$ 高さ $\textcolor{blue}{×}$ $\textcolor{blue}{\frac{1}{3}}$ $6$ $×$ $5$ $×$ $8$ $×$ $\frac{1}{3}$ $=\textcolor{red}{\rm 80 cm^3}$
(3) 円柱
底面積 $\textcolor{blue}{×}$ 高さ 直径が $6 \rm cm$ なので、半径は $3 \rm cm$
$3$ $×$ $3$ $×$ $\textcolor{blue}{π}$ $×$ $6$ $=\textcolor{red}{\rm 54π cm^3}$
POINT:円を含むときは $\textcolor{blue}{π}$ があるか確認

(4) 円錐
底面積 $\textcolor{blue}{×}$ 高さ $\textcolor{blue}{×}$ $\textcolor{blue}{\frac{1}{3}}$ $3$ $×$ $3$ $×$ $π$ $×$ $4$ $×$ $\frac{1}{3}$ $=\textcolor{red}{\rm 12π cm^3}$
(5) 三角柱(三角柱を横に倒した図形)
底面積 $\textcolor{blue}{×}$ 高さ $6×8$ $×$ $\frac{1}{2}$ $×$ $10$ $=\textcolor{red}{\rm 240cm^3}$
(6) 四角柱(底面:台形)
底面積 $\textcolor{blue}{×}$ 高さ
台形の面積:(上底 $\textcolor{blue}{+}$ 下底) $\textcolor{blue}{×}$ 高さ$\textcolor{blue}{÷}$ $\textcolor{blue}{2}$
$(3+7)$ $×$ $3$ $÷$ $2$ $×$ $6$ $=10×3÷2×6$ $=$ $\textcolor{red}{\rm 90 cm^3}$
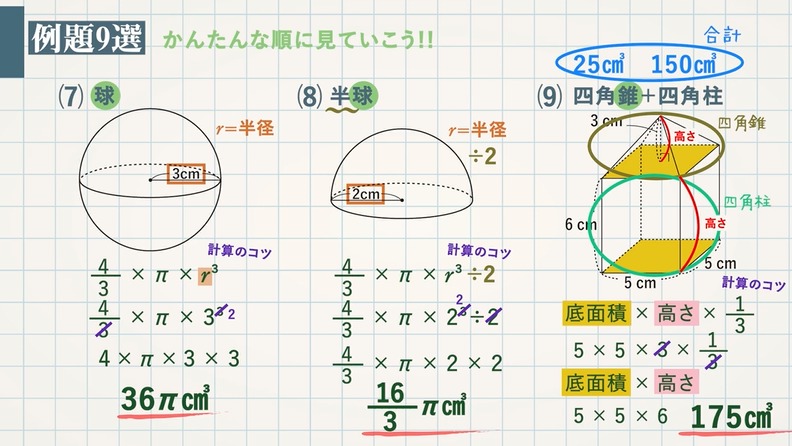
(7) 球
$\textcolor{blue}{\frac{4}{3}×π×r^3}$ $r(半径)=3 \rm cm$
$\frac{4}{3}$ $×$ $π$ $3^2$ $=$ $4$ $×$ $π$ $×$ $3$ $×$ $3$ $=\textcolor{red}{\rm 36π cm^3}$
(8) 半球 (半球なので $\textcolor{green}{÷2}$ )
$\textcolor{blue}{\frac{4}{3}×π×r^3÷2}$ $r(半径)=2 \rm cm$
$\frac{4}{3}$ $×$ $π$ $×$ $2^3$ $÷2$ $=$ $\frac{4}{3}$ $×$ $π$ $×$ $2$ $×$ $2$ $=\textcolor{red}{\rm \frac{16}{3}π cm^3}$
(9) 四角錐 $\textcolor{green}{+}$ 四角柱 (底面は同じ大きさ)
【四角錐】
底面積 $\textcolor{blue}{×}$ 高さ $\textcolor{blue}{×}$ $\textcolor{blue}{\frac{1}{3}}$ $5$ $×$ $5$ $×$ $3$ $×$ $\frac{1}{3}$ $=\textcolor{blue}{\rm 25 cm^3}$
【四角柱】
底面積 $\textcolor{blue}{×}$ 高さ $5×5$ $×$ $6$ $=\textcolor{blue}{\rm 150cm^3}$
【合計】
$\textcolor{blue}{\rm 25cm^3+150cm^3}=\textcolor{red}{\rm 175cm^3}$
コンテンツやシステムに関するお問い合わせ・オファーはこちらから