三平方の空間図形の問題には、大きく分けると $2$ 種類の問題タイプがあります。
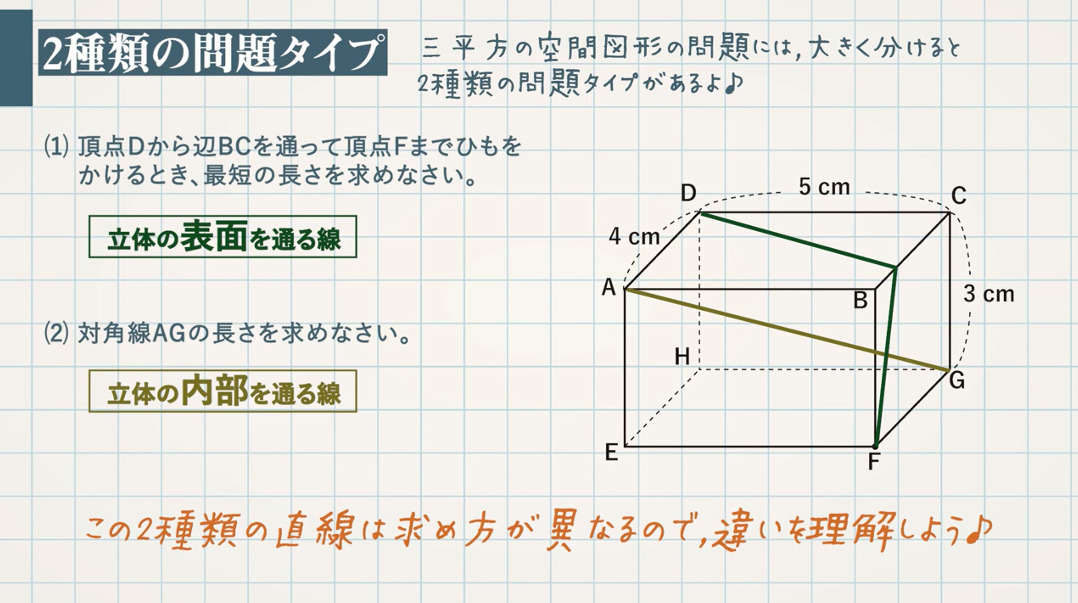
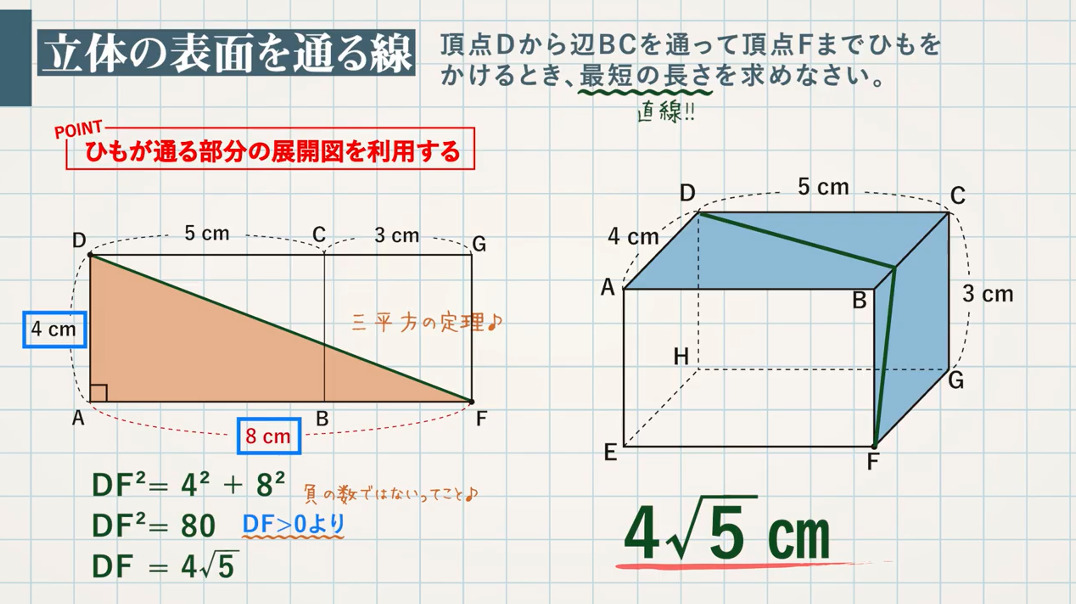
(1) 頂点 $\textcolor{green}{\rm D}$ から辺 $\textcolor{green}{\rm BC}$ を通って頂点 $\textcolor{green}{\rm F}$ までひもをかけるとき、最短の長さを求めなさい。
→立体の表面を通る線の長さを求める問題
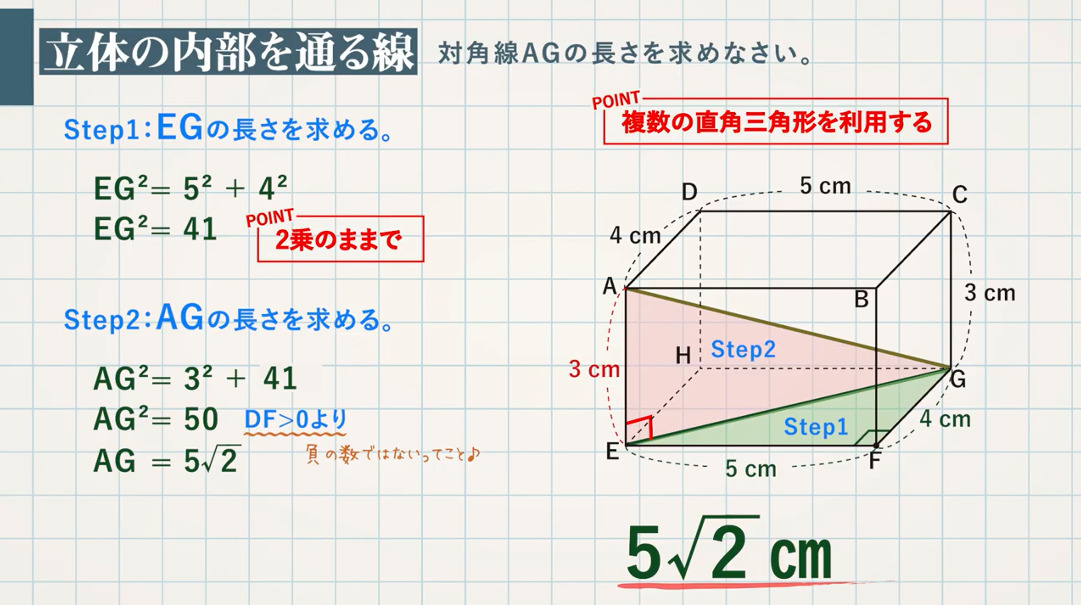
(2) 対角線 $\textcolor{green}{\rm AG}$ の長さを求めなさい。
→立体の内部を通る線の長さを求める問題
この $2$ 種類の直線は求め方が異なるので、違いを理解しましょう。