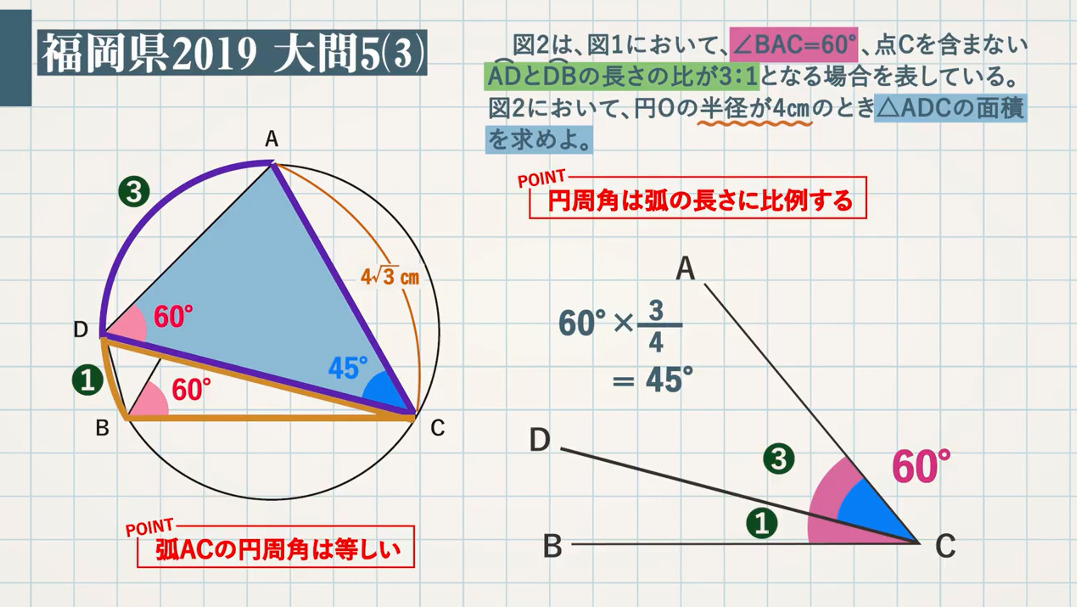
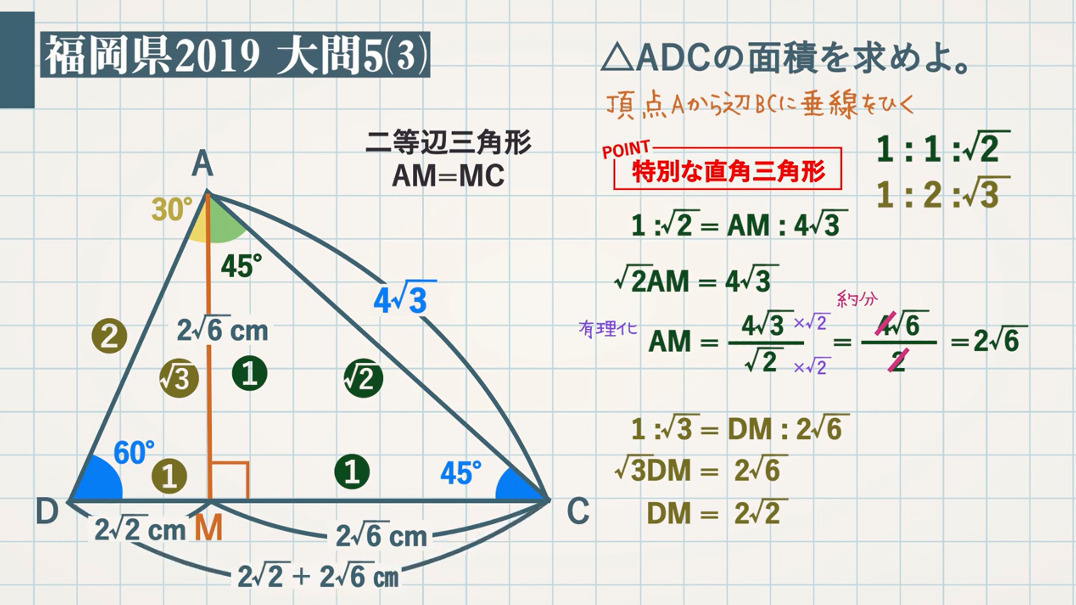
図 $\textcolor{green}{2}$ は、図 $\textcolor{green}{1}$ において、$\textcolor{green}{\rm ∠BAC=60°}$、点$\textcolor{green}{\rm C}$ を含まない $\textcolor{green}{\stackrel{\frown}{\rm AD}}$ と $\textcolor{green}{\stackrel{\frown}{\rm DB}}$ の長さの比が $\textcolor{green}{3:1}$ となる場合を表している。図 $\textcolor{green}{2}$ において、円 $\textcolor{green}{\rm  O}$ の半径が $\textcolor{green}{4\rm cm}$のとき、$\textcolor{green}{\rm △ADC}$ の面積を求めなさい。

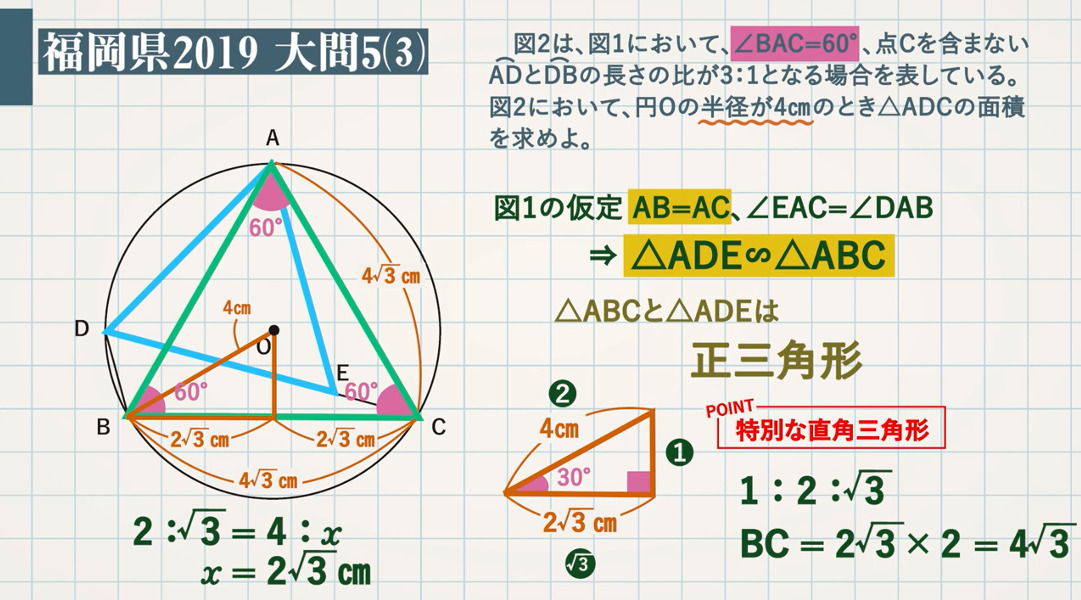
図 $1$ の仮定 $\rm AB=AC$,$\rm ∠EAC=∠DAB$ より、$\textcolor{blue}{\rm △ADE∽△ABC}$ であり、$\rm AB=AC$,$\rm 2BAC=60°$ より、$\textcolor{blue}{\rm △ABC}$,$\textcolor{blue}{\rm △ADE}$ は正三角形だとわかります。

POINT：特別な直角三角形（$\textcolor{blue}{1:2:\sqrt{3}} $)

$\rm BO$ (斜辺) $=\rm 4cm$ の特別な直角三角形なので、$2:\sqrt{3}=4:\rm \frac{1}{2}BC$　これを解いて、$\textcolor{blue}{\rm BC=4\sqrt{3} cm }$ 。

△ABCは正三角形なので、$\textcolor{blue}{\rm AC=4\sqrt{3} cm}$ となります。

POINT：円周角は弧の長さに比例する

$\stackrel{\frown}{\rm AD}$ と$\stackrel{\frown}{\rm DB}$ の長さの比が $3:1$ なので、円周角の大きさも  $3:1$ となります。

$\rm ∠ACD=∠DCB=3:1$

$\rm ∠ACB=60°$ より、$\rm ∠ACD=60°×\frac{3}{4}=\textcolor{blue}{45°}$

POINT：同じ弧に対する円周角は等しい。

$\stackrel{\frown}{\rm AC}$ に対する円周角は等しいので、$\rm ∠ABC=60°$ より、$\textcolor{blue}{\rm ∠ADC=60°}$ となります。 

頂点 $\rm A$ から辺 $\rm DC$ に垂線をひく。

POINT：特別な直角三角形（$\textcolor{blue}{1:1:\sqrt{2}}$)($\textcolor{blue}{1:2:\sqrt{3}} $)

$\rm △ADC$ の高さ $\rm AM$ を求める。

$\rm 1:\sqrt{2}=AM:4\sqrt{3}$　$\rm \textcolor{blue}{AM=2\sqrt{6} cm}$

$\rm △ADC$ の底辺 $\rm DC$ を求める。

$\rm △AMC$ は、$\rm AM=MC$ の直角二等辺三角形なので、$\rm MC=2\sqrt{6} cm$。$\rm △ADM$ は特別な直角三角形なので、$\rm 1:\sqrt{3}=DM:3\sqrt{6}$　これを解いて、$\rm DM=2\sqrt{2} cm$

よって、$\textcolor{blue}{\rm DC=DM+MC=2\sqrt{2}+2\sqrt{6}cm}$

$\rm △ADC$ の面積は、底辺$(\rm DC)×$ 高さ$(\rm AM)×\frac{1}{2}$ なので、 

$\textcolor{blue}{(2\sqrt{2}+2\sqrt{6})×(2\sqrt{6})×\frac{1}{2}}$　これを解いて、$\textcolor{red}{\rm 4\sqrt{3}+12 cm^2}$