高校では、樹形図を描かなくても何通りあるか求める方法である順列 $\rm P$ と組合せ $\rm C$ を習います。まずは $2$ つの違いを確認しましょう。

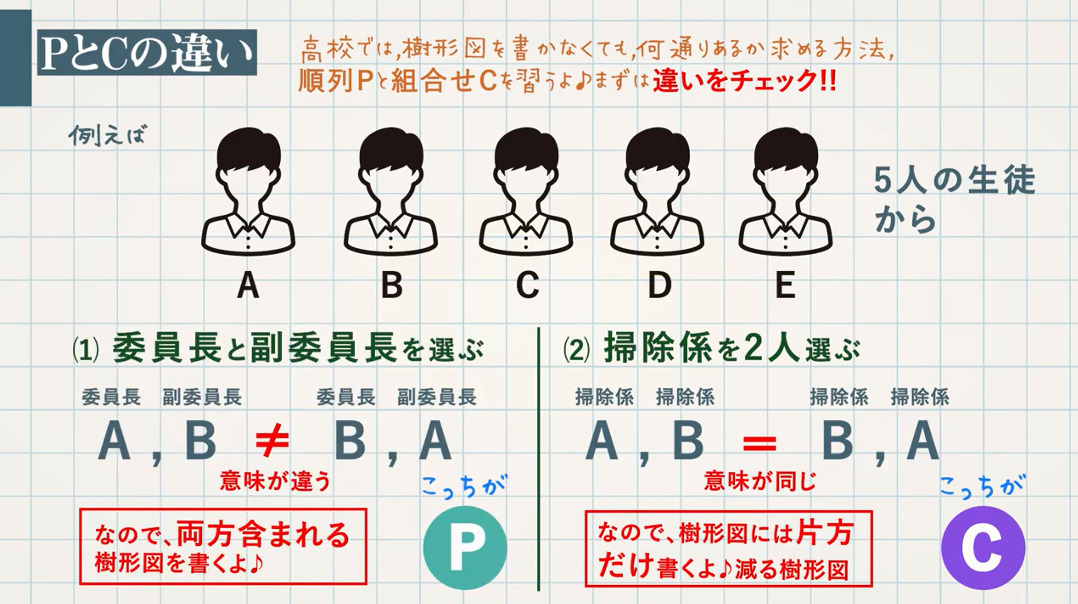
$\textcolor{green}{5}$ 人の生徒から

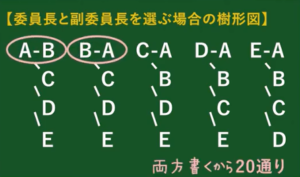
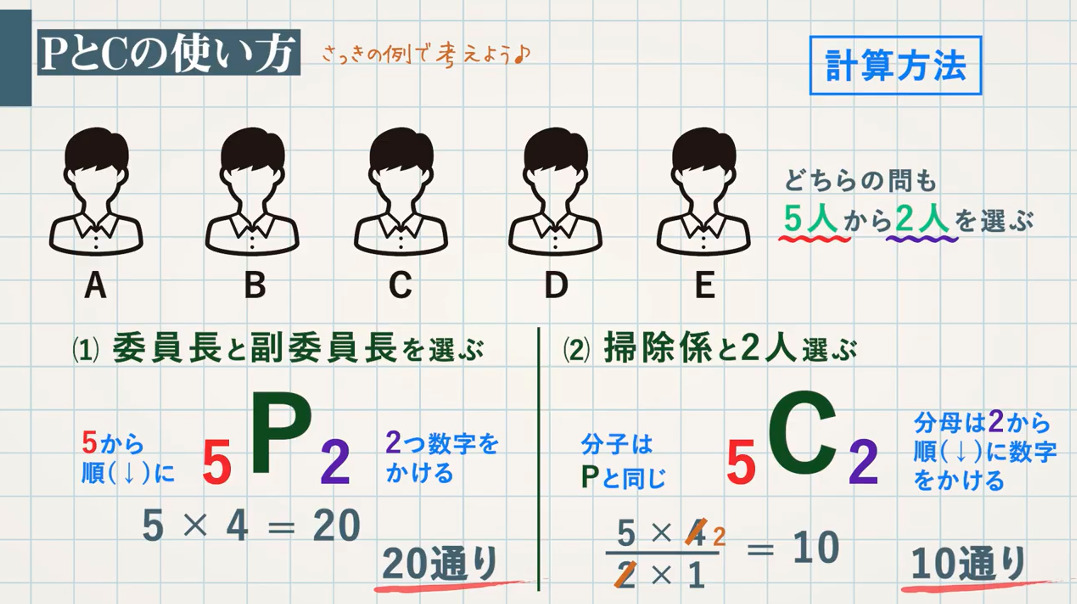
(1) 委員長と副委員長を選ぶ

「$\rm A$ が委員長で $\rm B$ が副委員長」と「$\rm B$ が委員長で $\rm A$ が副委員長」は意味が違うので、両方含まれる樹形図（左図）を書きます。（こっちが$\textcolor{blue}{\rm P}$）

(2) 掃除係を $\textcolor{green}{2}$ 人選ぶ

「掃除係 $\rm A$ と掃除係 $\rm B$」と「掃除係 $\rm B$ と掃除係 $\rm A$」は意味が同じなので、$\textcolor{blue}{片方だけの減る樹形図（右図）}$を書きます。（こっちが $\textcolor{blue}{\rm C}$）

さっきの例で、$\rm P$ と $\rm C$ の計算方法について確認しましょう。どちらの問も $\textcolor{blue}{5}$ 人から $\textcolor{blue}{2}$ 人を選びます。

(1) 委員長と副委員長を選ぶ

　　\begin{eqnarray*} && \textcolor{blue}{{}_5 \rm P _2} 　5 から順に 2 つの数をかける。\\&　&→ 5×4=20　　\textcolor{red}{20通り}\end{eqnarray*}

(2) 掃除係を $\textcolor{green}{2}$ 人選ぶ

　　\begin{eqnarray*} && \textcolor{blue}{{}_5 \rm C _2}　分子は\rm P と同じ。分母は2から順に数をかける。\\&　&→\frac{5×4}{2×1}=10　\textcolor{red}{10通り}\end{eqnarray*}

問題を解いて理解を深めましょう。

\begin{eqnarray*}\textcolor{green}{(3) {}_6 \rm P _4}　\textcolor{blue}{6}×5×4×3=\textcolor{red}{360通り}\end{eqnarray*}

\begin{eqnarray*}\textcolor{green}{(4) {}_5 \rm C _3}　\frac{\textcolor{blue}{5}×4×3}{\textcolor{blue}{3}×2×1}=\textcolor{red}{10通り}\end{eqnarray*}

\begin{eqnarray*}\textcolor{green}{(5) {}_5 \rm P _5}　\textcolor{blue}{5}×4×3×2×1=\textcolor{red}{120通り}\end{eqnarray*}

\begin{eqnarray*}\textcolor{green}{(6) {}_{10} \rm C _4}　\frac{\textcolor{blue}{10}×9×8×7}{\textcolor{blue}{4}×3×2×1}=\textcolor{red}{210通り}\end{eqnarray*}

このような問題にも使うことができます。

【問題】図の六角形の頂点を結んでできる三角形は全部で何個ありますか。

$\rm △ABD$ と $\rm △DBA$ は頂点の順番が違うだけで意味は同じになります。→ $\textcolor{blue}{\rm C}$ を使って計算。

$\textcolor{blue}{6}$ つの頂点から $\textcolor{blue}{3}$ つを選ぶので、

\begin{eqnarray*}{}\textcolor{blue}{_6 \rm C _3}　\frac{\textcolor{blue}{6}×5×4}{\textcolor{blue}{3}×2×1}=\textcolor{red}{20通り}\end{eqnarray*}