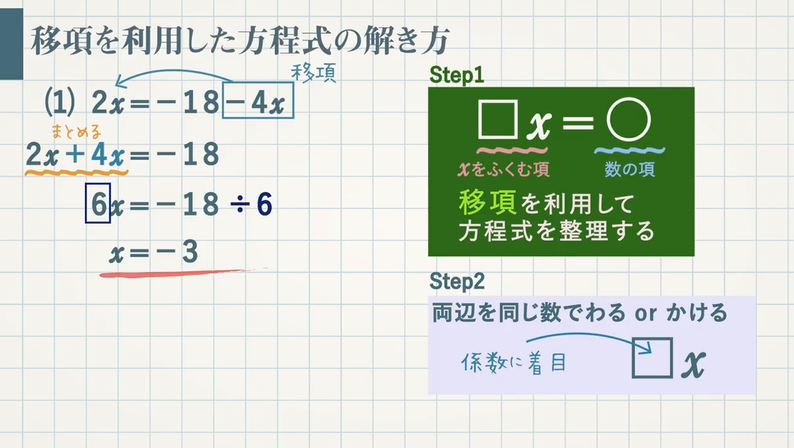
等式の性質と移項について確認しましょう。

${\rm A}+{\rm C}={\rm B}$ という式を ${\rm A}=□$ と変形するとき、

\begin{eqnarray}{\rm A}+{\rm C}&=&{\rm B}　 　 　・・・①\\ {\rm A}+{\rm C}\textcolor{blue}{-{\rm C}}&=&{\rm B}\textcolor{blue}{-{\rm C}}　・・・②\\{\rm A}&=&{\rm B}\textcolor{blue}{-{\rm C}}　・・・③ \end{eqnarray}

①と③の式を比べると、${\rm +C}$ の符号が変わって($-{\rm C}$ が)他方の辺に移っていることがわかります。このことを移項 (項を他辺に移す) といいます。

\begin{eqnarray} 　x+2&=&6\\ x&=&6\textcolor{blue}{-2} \end{eqnarray}

【問題】次の方程式を解きなさい。

\begin{eqnarray}\textcolor{green}
{(1)　2x}\textcolor{green}{=}\textcolor{green}
{-18-4x}\\\end{eqnarray}

STEP $\textcolor{blue}{1}$ ：□$\textcolor{blue}{x=〇}$ の形に移項を利用して変形

STEP $\textcolor{blue}{2}$ ：両辺を同じ数でわる or かける

\begin{eqnarray}2x&=&-18-4x\\ 2x\textcolor{blue}{+4x}&=&-18\\ 6x&=&-18　\textcolor{blue}{両辺を÷6}\\ \textcolor{red}{x}&\textcolor{red}{=}&\textcolor{red}{-3} \end{eqnarray}

\begin{eqnarray} \textcolor{green}{(2)　7x-9=4x+15}\end{eqnarray} 

STEP $\textcolor{blue}{1}$ ：□$\textcolor{blue}{x=〇}$ の形に移項を利用して変形

STEP $\textcolor{blue}{2}$ ：両辺を同じ数でわる or かける

\begin{eqnarray}7x-9&=&4x+15\\ 7x\textcolor{blue}{-4x}&=&15\textcolor{blue}{+9}\\ 3x&=&24　\textcolor{blue}{両辺を÷3}\\ \textcolor{red}{x}&\textcolor{red}{=}&\textcolor{red}{8} \end{eqnarray}