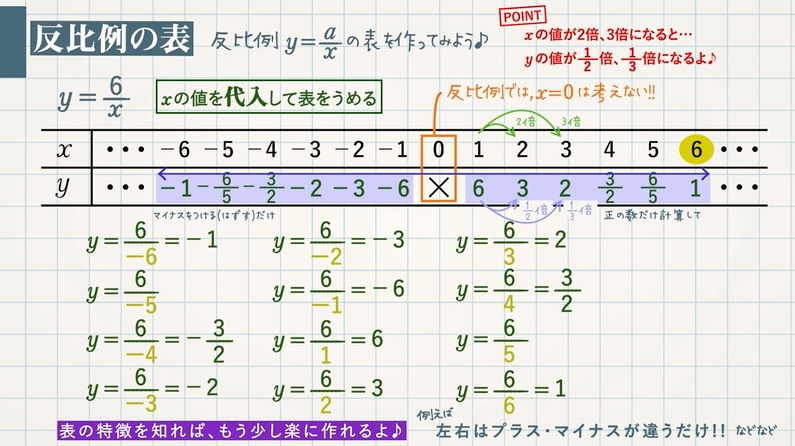
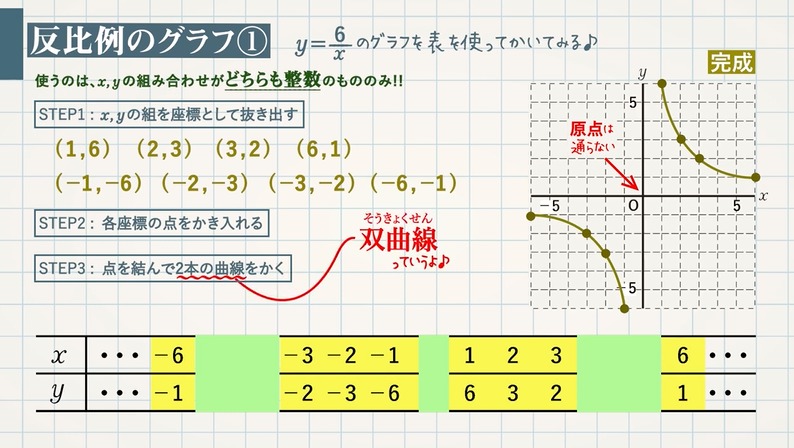
反比例 $y=\frac{6}{x}$ の表を作ってみましょう。$x$ の値を代入して表をうめます。

※反比例では、$\textcolor{blue}{x=0}$ は考えない

・$x$ が $\textcolor{blue}{-1}$ → $y=\frac{6}{-1}=\textcolor{blue}{-6}$　　・$x$ が $\textcolor{blue}{1}$ → $y=\frac{6}{1}=\textcolor{blue}{6}$

・$x$ が $\textcolor{blue}{-2}$ → $y=\frac{6}{-2}=\textcolor{blue}{-3}$　　・$x$ が $\textcolor{blue}{2}$ → $y=\frac{6}{2}=\textcolor{blue}{3}$

・$x$ が $\textcolor{blue}{-3}$ → $y=\frac{6}{-3}=\textcolor{blue}{-2}$　　・$x$ が $\textcolor{blue}{3}$ → $y=\frac{6}{3}=\textcolor{blue}{2}$

・$x$ が $\textcolor{blue}{-4}$ → $y=\frac{6}{-4}=\textcolor{blue}{-\frac{3}{2}}$　  ・$x$ が $\textcolor{blue}{4}$ → $y=\frac{6}{4}=\textcolor{blue}{\frac{3}{2}}$

・$x$ が $\textcolor{blue}{-5}$ → $y=\textcolor{blue}{-\frac{6}{5}}$　　　　   ・$x$ が $\textcolor{blue}{5}$ → $y=\textcolor{blue}{\frac{6}{5}}$

・$x$ が $\textcolor{blue}{-6}$ → $y=\frac{6}{-6}=\textcolor{blue}{-1}$　　・$x$ が $\textcolor{blue}{6}$ → $y=\frac{6}{6}=\textcolor{blue}{1}$

反比例の表の特徴（左右はプラスマイナスが違うだけ等）を知れば、もう少し楽に作れます。

POINT：$\textcolor{blue}{x}$ の値が $\textcolor{blue}{2}$ 倍、$\textcolor{blue}{3}$ 倍…になると $\textcolor{blue}{y}$ の値が $\textcolor{blue}{\frac{1}{2}}$ 倍、$\textcolor{blue}{\frac{1}{3}}$ 倍…になる。

$y=\frac{6}{x}$ のグラフを表を使って書いてみましょう。

使うのは、$x,y$ の組み合わせがどちらも整数のもののみとなります。($x$ が $5$ のとき、$y=\frac{6}{5}$ などは使わない)

STEP $\textcolor{blue}{1}$：$\textcolor{blue}{x,y}$ の組を座標として抜き出す

($1,6$)　($2,3$)　($3,2$)　($6,1$)

($-1,-6$)　($-2,-3$)　($-3,-2$)　($-6,-1$)

STEP $\textcolor{blue}{2}$：各座標の点をかき入れる

STEP $\textcolor{blue}{3}$：点を結んで $\textcolor{blue}{2}$ 本の曲線をかく

反比例のグラフは原点を通りません。また、$2$ 本の曲線でできているので双曲線といいます。

表がない場合の各座標の求め方を確認しておきましょう。

【例】$y=-\frac{12}{x}$

$\textcolor{blue}{x×y=a}$ より、かけて $\textcolor{blue}{-12}$ になる数の組を考えます。

$x=-12,y=1$ $\textcolor{blue}{(-12,1)}$　　$x=-6,y=2$ $\textcolor{blue}{(-6,2)}$　

$x=-4,y=3$ $\textcolor{blue}{(-4,3)}$　　　$x=-3,y=4$ $\textcolor{blue}{(-3,4)}$　

$x=-2,y=6$ $\textcolor{blue}{(-2,6)}$　　　$x=-1,y=12$ $\textcolor{blue}{(-1,12)}$　

$\textcolor{blue}{x,y}$ の数字を入れ替えます。

$x=1,y=-12$ $\textcolor{blue}{(1,-12)}$　　$x=2,y=-6$ $\textcolor{blue}{(2,-6)}$　

$x=3,y=-4$ $\textcolor{blue}{(3,-4)}$　　　$x=4,y=-3$ $\textcolor{blue}{(4,-3)}$　

$x=6,y=-2$ $\textcolor{blue}{(6,-2)}$　　　$x=12,y=-1$ $\textcolor{blue}{(12,-1)}$　

これで $12$ 組すべての座標がわかるので、グラフをかくことができます。

次はグラフから式を求める方法を確認しましょう。

これは、反比例の定数 $\textcolor{blue}{a=xy}$ を使えばすごく簡単です。

【例題】次の(1)～(3)のグラフの式を求めなさい。

STEP $\textcolor{blue}{1}$：曲線上に点を $\textcolor{blue}{1}$ つとり、座標を求める

(1) $(3,4)$　　(2) $(-4,4)$　　(3) $(2,2)$

STEP $\textcolor{blue}{2}$：座標から比例定数($\textcolor{blue}{a}$)を求める

(1) $a=3×4=\textcolor{blue}{12}$　　(2) $a=-4×4=\textcolor{blue}{12}$　　(3) $a=2×2=\textcolor{blue}{4}$

STEP $\textcolor{blue}{3}$：反比例の式 ($\textcolor{blue}{y=\frac{a}{x}}$) に $\textcolor{blue}{a}$ の値を入れる。 

(1) $\textcolor{red}{y=\frac{12}{x}}$　　(2) $\textcolor{red}{y=-\frac{16}{x}}$　　(3) $\textcolor{red}{y=\frac{4}{x}}$