面積が $\textcolor{green}{24 \rm cm^2}$ の長方形で、底辺の長さを $\textcolor{green}{x \rm cm}$ , 高さを $\textcolor{green}{y\rm cm}$ とする。

底辺($\rm cm$) $×$ 高さ($\rm cm$) $=$ 長方形の面積($\rm cm^2$)

　　$x$　   $×$　　$y$ 　   $=$　　$24$

\begin{eqnarray} y を x の式で表すと、\textcolor{red}{y=\frac{24}{x}} \end{eqnarray}

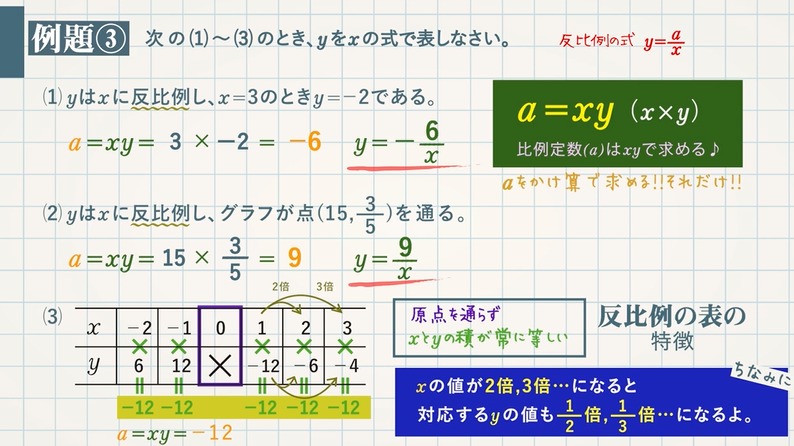
このように $y$ が $x$ の関数であり、$\textcolor{blue}{y=\frac{a}{x}}$ の関係が成り立つとき、$y$ は $x$ に反比例するといいます。

反比例では、$xy（x×y）$ は常に一定$\textcolor{blue}{（a）}$になります。

$x$ が $2$ のとき、$y$ は $\textcolor{blue}{12}$ （$2×12=\textcolor{blue}{24}$） 

$x$ が $3$ のとき、$y$ は $\textcolor{blue}{8}$   （$3×8=\textcolor{blue}{24}$）

$x$ が $4$ のとき、$y$ は $\textcolor{blue}{4}$   （$4×6=\textcolor{blue}{24}$）

次のア～オの中から、$\textcolor{green}{y}$ が $\textcolor{green}{x}$ に反比例するものをすべて選びなさい。

ア　$y=\frac{8}{x}$　　　 イ　$\frac{y}{3}=-5x$　　　ウ　$xy=-2$

エ　$\frac{y}{x}=9$　　　 オ　$y=\frac{x}{5}$

ア→〇　比例定数 $\textcolor{blue}{8}$

イ→✕　変形すると、$y=-15x$　比例($\textcolor{blue}{y=ax}$) の形です。

ウ→〇　変形すると、 $y=-\frac{2}{x}$　比例定数 $\textcolor{blue}{-2}$

エ→✕　変形すると、$y=9x$　比例($\textcolor{blue}{y=ax}$) の形です。

オ→✕　$y=\frac{x}{5}=y → y=\frac{1}{5}x$　比例($\textcolor{blue}{y=ax}$) の形です。

$\textcolor{green}{y}$ は $\textcolor{green}{x}$ に反比例し、$\textcolor{green}{x=5}$ , $\textcolor{green}{y=6}$ である。次の問いに答えなさい。

(1) 比例定数を求めなさい。

$a=xy=5×6=\textcolor{red}{30}$

(2) $\textcolor{green}{y}$ を $\textcolor{green}{x}$ の式で表しなさい。

$a$ の値を (1) で求めているので、反比例の形（$y=\frac{a}{x}$）にするだけです。$\textcolor{red}{y=\frac{30}{x}}$

(3) $\textcolor{green}{x=-2}$ のとき、$\textcolor{green}{y}$ の値を求めなさい。

$x=-2$ を (2) 式に代入して求めます。

$y=30÷(-2)=\textcolor{red}{-15}$

※重要

$a=xy$ を変形すると、$\textcolor{blue}{x=\frac{a}{y}（a÷y）}$

$x$ の値は、$y$ の値を求めるときと同様、定数 $\textcolor{blue}{a}$ をわって求めることができます。

次の (1) ～ (3) のとき、$\textcolor{green}{y}$ を $\textcolor{green}{x}$ の式で表しなさい。

(1) $\textcolor{green}{y}$ は $\textcolor{green}{x}$ に反比例し、$\textcolor{green}{x=3}$ のとき $\textcolor{green}{y=-2}$ である。

$a=xy=3×-2=\textcolor{blue}{-6}$　$\textcolor{red}{y=-\frac{6}{x}}$

(2) $\textcolor{green}{y}$ は $\textcolor{green}{x}$ は反比例し、グラフが点（$\textcolor{green}{15,\frac{3}{5}}$）を通る。

$a=xy=15×\frac{3}{5}=\textcolor{blue}{9}$　$\textcolor{red}{y=\frac{9}{x}}$

(3) 原点を通らず $\textcolor{green}{x}$ と $\textcolor{green}{y}$ の積が一定→反比例の表の特徴

$a=xy=\textcolor{blue}{-12}$　$\textcolor{red}{y=-\frac{12}{x}}$

反比例では、$\textcolor{blue}{x}$ の値が $\textcolor{blue}{2倍}$ , $\textcolor{blue}{3倍}$… になると対応する $\textcolor{blue}{y}$ の値は $\textcolor{blue}{\frac{1}{2}倍}$ , $\textcolor{blue}{\frac{1}{3}倍}$… になります。