平面上の点の位置は、$2$ つの数の組を使って表すことができます。

まずは、直角に交わる $2$ 本の数直線について確認しておきましょう。

ヨコの数直線を $\textcolor{blue}{x}$ 軸（横軸）

タテの数直線を $\textcolor{blue}{y}$ 軸（横軸）

$\textcolor{blue}{x}$ 軸と$\textcolor{blue}{y}$ 軸をあわせて座標軸といいます。

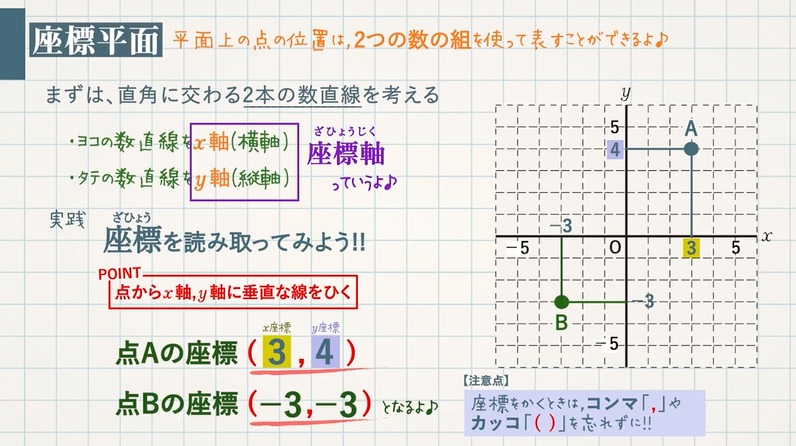
【実践】図のA,Bの座標を読み取ってみましょう。

POINT：点から $\textcolor{blue}{x}$ 軸 , $\textcolor{blue}{y}$ 軸に垂直な線をひく

点Aから $x$ 軸 , $y$ 軸に垂直な線をひくと、$x$ 座標が $\textcolor{blue}{3}$ , $y$ 座標が $\textcolor{blue}{4}$ なので、

点Aの座標 （$\textcolor{red}{3}$ , $\textcolor{red}{4}$）

点Bから $x$ 軸 , $y$ 軸に垂直な線をひくと、$x$ 座標が $\textcolor{blue}{-3}$ , $y$ 座標が $\textcolor{blue}{-3}$ なので、

点Bの座標 （$\textcolor{red}{-3}$ , $\textcolor{red}{-3}$）

比例のグラフの書き方をかんたんな方法で確認しましょう。

STEP $\textcolor{blue}{1}$ :比例定数($\textcolor{blue}{a}$)を分数にする

STEP $\textcolor{blue}{2}$ :点を $\textcolor{blue}1$ つとる　※スタートは原点 

STEP $\textcolor{blue}{3}$ : $\textcolor{blue}{2}$ 点をふくむ直線をひく。

(1) $\textcolor{green}{y=3x}$

\begin{eqnarray}\newline \textcolor{blue}{\frac{3 ← y の増加量(タテ)}{1← x の増加量(ヨコ)}} 　座標(3,1)と原点を通る直線\end{eqnarray}

(2) $\textcolor{green}{y=-x}$

\begin{eqnarray}\newline \textcolor{blue}{\frac{-1 ← y の増加量(タテ)}{1← x の増加量(ヨコ)}}　座標(1,-1)と原点を通る直線 \end{eqnarray}

(3) $\textcolor{green}{y=-\frac{2}{3}x}$

\begin{eqnarray}\newline \textcolor{blue}{\frac{-2 ← y の増加量(タテ)}{3← x の増加量(ヨコ)}}　座標(3,-2)と原点を通る直線 \end{eqnarray}

次にグラフから、式を求めてみましょう。

STEP $\textcolor{blue}{1}$ :直線上の座標を $\textcolor{blue}{1}$ つとる

($\textcolor{blue}{y}$ 軸より右側に座標をとる方がかんたん)

STEP $\textcolor{blue}{2}$ :比例定数 ($a$) を求める

(1) グラフは $\textcolor{blue}{(3,2)}$ を通るので、

\begin{eqnarray} a=\frac{y の増加量}{x の増加量}=\textcolor{blue}{\frac{2}{3}}　よって、\textcolor{red}{y=\frac{2}{3}x} \end{eqnarray}

(2) グラフは $\textcolor{blue}{(1,-2)}$ を通るので、

\begin{eqnarray} a=\frac{y の増加量}{x の増加量}=\textcolor{blue}{\frac{-2}{1}}=\textcolor{blue}{-2}　よって、\textcolor{red}{y=-2x} \end{eqnarray}